Name                                     

MATH 204 PRACTICE MIDTERM III

Please work out each of the given problems on your own paper.  Credit will be based on the steps that you show towards the final answer.  Show your work.  

Printable Key

Problem 1 
Solve the given differential equation by means of a power series about x = 0.  Find a recurrence relation and write the final solution in the form

        y'' + xy' + 2y  =  0,        y(0)  =  0,     y'(0)  =  1

Solution

Problem 2 

Determine the general solution of the differential equation that is valid in any interval not including the singular point. 

        x²y'' - xy' + y  =  0      

         Solution                                               

Problem 3 

Solve the following differential equation

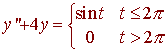
            y(0)  =  y'(0)  =  0

  Solution

Problem 4 

Find the general solution of the given system of equations and describe the behavior of the solution as .

   Solution

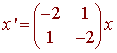
Problem 5 

An electric circuit  is describes by the system of differential equations

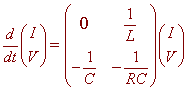
A.     Suppose that R = 1 ohm, C = ½ farad, and L = 1 henry.  Find the general solution of the system in this case.

Solution

B.      Find I(t) and V(t) if I(0) = 2 amperes and V(0) = 1 volt.

Solution

C.     For the circuit of part A. determine the limiting values of I(t) and V(t) as .  Do these limiting values depend on the initial conditions?  

        Solution

Problem 6  Please answer the following true or false.  If true, explain why.  If false, explain why or provide a counter-example.

A.    If  f(x)  is a function that is not continuous at x  =  2 , then the Laplace transform of  f(x)  is also not continuous at x =  2 .  

Solution

B.   Let      be a solution of the differential equation

            x                     1  
              y''  +                y'  + (sin x)y  =  0
    x + 4              x - 2                

 then  x  =  -1  is in the interval of convergence of y(x).  

Solution