Name
MATH 204 PRACTICE MIDTERM III
Please work out each of
the given problems on your own paper.
Credit will be based on the steps that you show towards the final answer.
Show your work.
Problem 1
Solve the given differential equation by means of a power series about x
= 0. Find
a recurrence relation and write the final solution in the form
![]()
y'' + xy' + 2y = 0, y(0) = 0, y'(0) = 1
![]()
Plugging back into the original differential equation gives
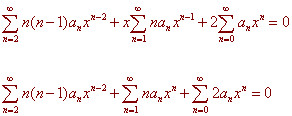
Now adjust the sums so that they all contain the same powers of x.
![]()
Now pull out the n = 0 term and combine the sums
![]()
Next use the initial conditions to get
a0 = 0 a1 = 1
2a2 + 2a0 = 0
Hence
a2 = 0
The recursion relationship gives
(n + 2)(n + 1)an+2 + (n + 2)an = 0
or
-an
an+2
=
n + 1
Hence all the even coefficients are 0. The odds are
-1
1
-1
1
a1 =
1 a3
=
a5 =
a7 =
a9 =
2
3. 4
3.
4. 6
3.
4. 6.
8
In general
(-1)n
(-1)n
a2n+1 =
=
2.
4. 6.
....
(2n)
2n n!
The
general solution is
![]()
Problem 2
Determine the general solution of the differential equation that is valid in any interval not including the singular point.
x2y'' - xy' + y = 0
![]()
![]()
We let
y = xr
Then
y' = rxr-1 y'' = r(r - 1)xr-2
Substituting back into the original equation gives
r(r - 1)xr - rxr + xr = 0
r2 - r - r + 1 = r2 - 2r + 1 = 0
(r - 1)2 = 0
r = 1 (repeated twice)
Hence
y = (c1 + c2 ln|x|) |xr|
![]()
Problem 3
Solve
the following differential equation
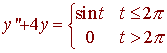
y(0) = y'(0) = 0
Since this is a piecewise defined differential equation, we use the method of Laplace Transforms.
L(y'') + 4L(y) = L(g) = L[sin t (1 - u2p(t)) = L(sin t) - L[(sin t) u2p(t)]
1
1
s2L(y)
+ 4L(y) =
- e-2ps
s2 +
1
s2 + 1
Solving for L(y), we get
1
L(y)
= (1 - e-2ps)
(s2 + 1)(s2 + 4)
Now use partial fractions
1
As + B Cs + D
=
+
(s2
+ 1)(s2 +
4) s2
+ 1 s2
+ 4
or
(As + B)(s2 + 1) + (Cs + D)(s2 + 4) = 1
As3 + Bs2 + As + B + Cs3 + Ds2 + 4Cs + 4D = 0
Equating coefficients gives
A + C = 0 B + D = 0 A + 4C = 0 B + 4D = 0
This has solution
A = 0 B = -1/3 C = 0 D = 1/3
Putting this together gives
1
1
1
L(y)
= (1 - e-2ps)
-
3
s2 +
4 s2
+ 1
1
1
1
e-2ps
e-2ps
L(y)
= (
-
-
+
)
3 s2 +
4 s2
+ 1 s2
+ 4 s2 +
1
Now take the inverse Laplace Transform to get
y = 1/3 ( sin(2t) - sin t - u2p sin(2t) + u2p sin t)
Problem 4
Find
the general solution of the given system of equations and describe the behavior
of the solution as
![]() .
.
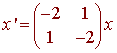
Find the eigenvalues and eigenvectors of the matrix.
![]()
= (-2 - l)(-2 - l) - 1 = l2 + 4l + 4 - 1
= l2 + 4l + 3 = (l + 3)(l + 1) = 0
Thus the eigenvalues are
l = -3 and l = -1
Now find the eigenvectors
v-3: Plugging in -3 for l, we get
![]()
Which has (1,-1) in its null space.
v-1: Plugging in -1 for l, we get
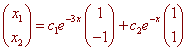
Which has (1,1) in its null space.
The solution is
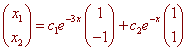
or
x1 = c1e-3x + c2e-x
x2 = -c1e-3x + c2e-x
Problem 5
An
electric circuit is describes by the system of differential equations
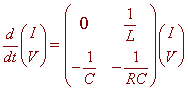
A.
Suppose that R = 1 ohm, C
= ½ farad, and L = 1 henry.
Find the general solution of the system in this case.
Plugging in the numbers we get the matrix
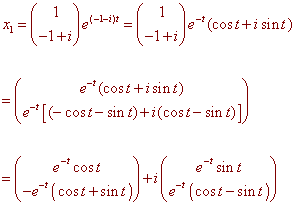
Now find the eigenvalues
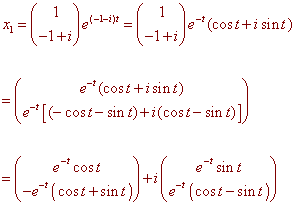
Take the determinant to get
(-l)(-2 - l) + 2 = l2 + 2l + 2 = 0
The roots of this quadratic are
-1 + i and -1 - i
v-1+i: Plugging in -1 + i for l, we get
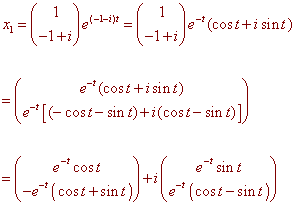
The first row gives
(1 - i)x + y = 0
y = (-1 + i)x
So the corresponding eigenvector is
v-1+i = (1,-1 + i)
We have
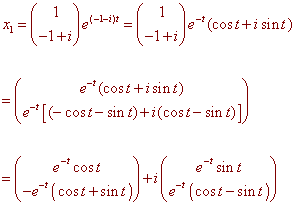
Hence the general solution is given by
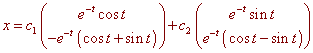
That is
I(t) = c1e-t cost + c2e-t sin t
V(t) = c1e-t(-cos t - sin t) + c2e-t (cos t - sin t)
B.
Find I(t) and V(t)
if I(0) = 2 amperes and V(0)
= 1 volt.
Plug in to get
0 = c1
1 = -c1 + c2
The solution is
I(t) = e-t sin t
V(t) = e-t (cos t - sin t)
C.
For the circuit of part A. determine the limiting values of I(t)
and V(t) as
.
Do these limiting values depend on the initial conditions?
Since the e-t term dominates all expressions, both the current and voltage will drop to zero as time approaches infinity independent of the initial conditions.
Problem 6
Please
answer the following true or false.
If true, explain why.
If false, explain why or provide a counter-example.
A.
If f(x)
is a
function that is not continuous at x = 2
, then the Laplace transform of f(x)
is also
not continuous at x = 2
.
False, consider u2(t) which is not continuous at 2. The Laplace transform is e-2s / s which is continuous at 2.
B.
Let
![]() be
a solution of the differential equation
be
a solution of the differential equation
x
1
y'' +
y' + (sin x)y = 0
x +
4
x -
2
then
x = -1 is in the interval of
convergence of y(x).
False, the solution converges inside (0,2) which does not contain -1.