Name                                    

 

MATH 204 PRACTICE FINAL

 

Please work out each of the given problems on your own paper.  Credit will be based on the steps that you show towards the final answer.  Show your work.

  Printable Key

Problem 1

Solve the following differential equations.

 

A.  (x2 + 1)y' + 4xy  =  x    y(0)  =  2 

Solution

B.  (yex + 2ex + y2)dx + (ex + 2xy)dy  =  0 

Solution

C.   y(iv) + 4y''  =  2    

Solution

D.                                    1
  y'' + 3y' + 2y  =                            (You may leave this as an integral)
                              1 + et

Solution

E.     (x2 + 1)y'' + xy' + y  =  0            y(0)  =  1,    y'(0)  =  0       

Solution

F.    x2y'' + 2xy' + y  =  0   

Solution

G.    

Solution

H.     x1'  =  4x1 + x2

        x2'  =  3x1 + 2x2

Solution

 

Problem 2  

Lake Tahoe holds 30 cubic kilometers and Fallen Leaf Lake holds 0.5 cubic kilometers.  It is estimated that there are currently 20 tons of trout in Lake Tahoe and 1 ton of trout in Fallen Leaf Lake.  Water flows from Fallen Leaf Lake to Lake Tahoe at 0.1 cubic kilometers per day.  Through an underground channel, water flows from Lake Tahoe to Fallen Leaf Lake at 0.01 cubic kilometers per day.  Water with 2 tons of trout per cubic kilometer flows into Fallen Leaf Lake from the desolation wilderness at a rate of 0.09 cubic kilometers per day.  Water flows out of Lake Tahoe into the Truckee River at a rate of 0.09 cubic kilometers per day.  Assume that when water flows out of either lake the density of the trout in the outflow is equal to the density of the trout in the lake that is the source of the outflow.  Set up a system of differential equations that model this situation.

Solution

Problem 3  

Given that y  =  x  is a solution of 

        (x2 + 1)y'' - 2xy' + 2y  =  0

Solution

find a linearly independent solution by reducing the order.

 

Problem 4 

A six Newton weight is attached to the lower end of a coil spring suspended from the ceiling, the spring constant of the spring being 27 Newtons per meter.  The weight comes to rest in its equilibrium position, and beginning at t = 0 and external force given by F(t)  =  12 cos(20t) is applied to the system.  Determine the resulting displacement as a function of time, assuming damping is negligible.

  Solution

 

Problem 5

Please answer the following true or false.  If false, explain why or provide a counter-example.  If true, explain why.

 

A.     If the lion population P(t) of Africa follows the differential equation

                P'(t)  =  -10P(10,000 - P)(30,000 - P)
             
and there are 20,000 lions in Africa today, then the lions will eventually become extinct in Africa.

Solution

B.     (15 Points) Let f(t)  =  sin(t2)e10t .  Then the Laplace transform of f(t)  is defined for all s > 10 .

Solution

C.     (15 Points) Suppose that y1(x) and y2(x) are differentiable functions and y'' + p(x)y' + q(x)y  =  0 
is a differential equation such that p(x) and q(x) are continuous functions. If the Wronskian of y1(x) and y2(x) is

                               e3x
            W  =                
                       1 + x2

 

     then y1(x) and y2(x) cannot be solutions to the differential equation.

Solution

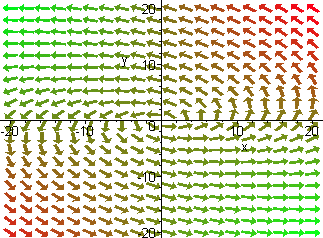
D.     (15 Points) Suppose that two-dimensional system x'  =  Ax of differential equations has the phase portrait pictured below.  Then the eigenvalues of A are real and distinct.

Solution