Name
MATH 204 PRACTICE FINAL
Please
work out each of the given problems on your own paper.
Credit will be based on the steps that you show towards the final answer.
Show your work.
Problem 1
Solve the
following differential equations.
A.
(x2 + 1)y' + 4xy
= x y(0) = 2
This equation is separable (also linear, but solving using separation of variables is usually easier). We have
x -
4xy
x
y' =
=
(1 -
4y)
x2 +
1 x2
+ 1
Separating, we get
dy
x
=
dx
1 -
4y x2
+ 1
Now integrate both sides to get
-1/4 ln|1 - 4y| = 1/2 ln(x2 + 1) + C1
ln|1 - 4y| = -2 ln(x2 + 1) + C1 = ln(x2 + 1) -2 + C1
|1 - 4y| = C(x2 + 1)2
B.
(yex + 2ex + y2)dx + (ex +
2xy)dy = 0
We have
My = ex + 2y = Nx
Hence this is an exact differential equation. We have
fx = yex + 2ex + y2
Integrating with respect to x, we get
f(x,y) = yex + 2ex + xy2 + C(y)
Taking the derivative with respect to y and setting it equal to N gives
fy(x,y) = ex + 2xy + C'(y) = ex + 2xy
Hence
C'(y) = 0
We can conclude that
yex + 2ex + x y2 = C
is the solution.
C.
y(iv) + 4y'' = 2
First we find the homogeneous solution by finding the roots of the characteristic polynomial
r4 + 4r2 = r2(r2 + 4) = 0
r = 0 (repeated twice) and r = 2i, r = -2i
The homogeneous solution is
yh = c1 + c2t + c3 cos(2t) + c4 sin(2t)
Next, we seek a particular solution. We use the method of undetermined coefficients. The UC set for g(t) is
{1}
Since this intersects with the homogeneous solution, we multiply by t2 (note that multiplying by t does not get it out of the homogeneous solution.) Let
yp = At2 yp' = 2At yp'' = 2A yp''' = yp(iv) = 0
Substituting back into the differential equation gives
0 + 4(2A) = 2
A = 1/4
The solution is
y = yh + yp = c1 + c2t + c3 cos(2t) + c4 sin(2t) + 1/4
D.
1
y'' + 3y' + 2y =
(You may
leave this as an integral)
1 + et
We first find the homogeneous solution by finding the roots of the characteristic polynomial
r2 + 3r + 2 = (r + 2)(r + 3) = 0
r = -2 or r = -3
The homogeneous solution is
yh = c1e-2t + c2e-3t
Since g(t) is not a UC function, we use the method of variation of parameters. We let
yp = v1e-2t + v2e-3t
Now find the Wronskian matrix and determinant.
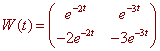
This matrix has determinant
W = -3e-5t + 2e-5t = -e-5t
The inverse of the Wronskian matrix is
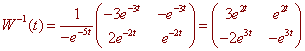
We get
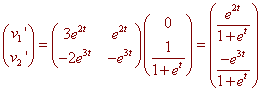
Now integrate and add to get
y = yh + yp
![]()
E. (x2 + 1)y'' + xy' + y = 0 y(0) = 1, y'(0) = 0
Solution
![]()
Plug these into the differential equation to get
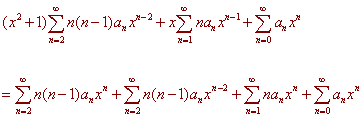
Next, change shift the index of summation in the second sum to get an xn.
![]()
Now pull out terms so that the summations all begin at n = 2.
![]()
From the initial conditions, we have
a0 = 1 a1 = 0
The pulled out terms from the series gives
2a2 + 1 = 0 a2 = -1/2
and
6a3 + 0 = 0 a3 = 0
Putting the sums together and setting the coefficients equal to zero gives
n(n - 1)an + (n + 2)(n + 1)an+2 + nan + an = 0
[n(n - 1) + n + 1]an + (n + 2)(n + 1)an+2 = 0
(n2 + 1)an + (n + 2)(n + 1)an+2 = 0
-(n2 + 1)an
an+2 =
(n + 2)(n + 1)
We see that all the odd terms will be 0. We use the recursion relationship to find the even terms.
5
a4
=
4.3.2
-37.5
a6
=
6.5.
4.3.2
(-1)n5.37 . ...
. ((2n)2
+ 1)
a2n
=
(2n)!
![]()
F. x2y'' + 2xy' + y = 0
Solution
y = xr
We find
F(r) = r2 + r + 1
This has complex roots
![]()
The general solution is
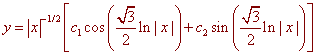
G.
![]()
We take the Laplace transform of both sides
L{y''} + 2L{y'} + 5L{y} = L{1 - up(t)}
s2L{y} + 2sL{y} + 5L{y} = 1/s - e-ps / s
(s2 + 2s + 5)L{y} = 1/s - e-ps / s
1
L{y} = (1 - e-ps)
s(s2 + 2s + 5)
Now use partial fractions
A
Bs +
C
1
+
=
s
s2 + 2s +
5
s(s2 + 2s + 5)
A(s2 + 2s + 5) + (Bs + C)s = 1
Let s = 0:
5A = 1 A = 1/5
We have
1/5 s2 + 2/5 s + 1 + Bs2 + Cs = 1
Hence
B = -1/5 and C = -2/5
We have
1
s +
1
3
5L{y} =
-
-
s (s + 1)2
+ 1 (s + 1)2 +
1
1
s +
1
3
+ e-ps(
-
-
)
s (s + 1)2
+ 1 (s + 1)2 + 1
y = 1/5(1 - etcos t - 3etsin t + up(t)(1 - et -pcos(t - p)- 3et - psin(t - p))
H. x1' = 4x1 + x2
x2' = 3x1 + 2x2
This is the system
![]()
Find the eigenvalues by finding the determinant of
![]()
The determinant is
(4 - r)(2 - r) - 3 = r2 - 6r + 5 = (r - 5)(r - 1)
The roots are
r = 1 and r = 5
Now plug in to find the eigenvectors. Plugging in 1 gives
![]()
which gives
3x1 + x2 = 0
So an eigenvalue is
![]()
Plugging in 5 gives
![]()
which gives
-x1 + x2 = 0
So an eigenvalue is
![]()
The solution is
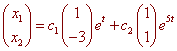
or
x1 = c1et + c2e5t
x2 = -3c1et + c2e5t
Problem 2
Lake Tahoe holds 30 cubic kilometers and Fallen Leaf Lake holds 0.5 cubic kilometers. It is estimated that there are currently 20 tons of trout in Lake Tahoe and 1 ton of trout in Fallen Leaf Lake. Water flows from Fallen Leaf Lake to Lake Tahoe at 0.1 cubic kilometers per day. Through an underground channel, water flows from Lake Tahoe to Fallen Leaf Lake at 0.01 cubic kilometers per day. Water with 2 tons of trout per cubic kilometer flows into Fallen Leaf Lake from the desolation wilderness at a rate of 0.09 cubic kilometers per day. Water flows out of Lake Tahoe into the Truckee River at a rate of 0.09 cubic kilometers per day. Assume that when water flows out of either lake the density of the trout in the outflow is equal to the density of the trout in the lake that is the source of the outflow. Set up a system of differential equations that model this situation.
A diagram is shown below
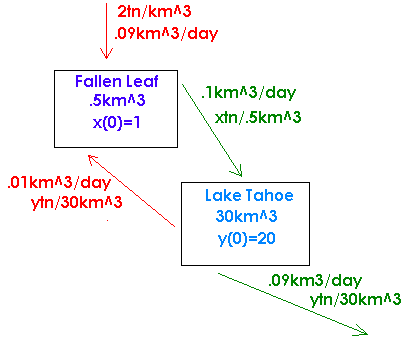
We use the equation
Rate = Rate In - Rate Out
For Fallen leaf (x tons of trout), we have
x' = (2(.09) + .01y/30) - (.1x / .5)
For Lake Tahoe, we have
y' = (.1x / .5) - (.01y / 30 + .09y / 30)
The differential equations reduce to
x' = .18 + y/3000 - x/5
y' = x/5 - y/300
x(0) = 1 y(0) = 20
Problem 3
Given that y = x is a solution of
(x2 + 1)y'' - 2xy' + 2y = 0
find
a linearly independent solution by reducing the order.
We use reduction of order
y = vx y' = v'x + v y'' = v''x + 2v'
Substituting into the original equation gives
(x2 + 1)(v''x + 2v') - 2x(v'x + v) + 2vx
= x3v'' + xv'' + 2x2v' + 2v' - 2x2v' - 2xv + 2xv
(x3 + x)v''+ 2v' = 0
Now let w = v' to get
(x3 + x)w'+ 2w = 0
We have
2w
w' =
x(x2 + 1)
dw
2
=
dx
w x(x2
+ 1)
Use partial fractions for the right hand side to get
A Bx +
C
2
+
=
x x2
+ 1 x(x2
+ 1)
A(x2 + 1) + (Bx + C)x = 2
Setting x = 0 gives
A = 2
We have
2x2 + 2 + Bx2 + Cx = 2
Hence
B = 2 and C = 0
This gives
ln(w) = ln(x) + ln(x2 + 1)
or
w = x3 + x
Integrate to get
v = 1/4 x4 + 1/2 x2
Hence, a second solution is
y = vx = 1/4 x5 + 1/2 x3
Problem 4
A six Newton weight is attached to the lower end of a coil spring suspended from the ceiling, the spring constant of the spring being 27 Newtons per meter. The weight comes to rest in its equilibrium position, and beginning at t = 0 and external force given by F(t) = 12 cos(20t) is applied to the system. Determine the resulting displacement as a function of time, assuming damping is negligible.
We have the differential equation
6y'' + 27y = 12cos(20t)
We have
F0 = 12, w0
= 3 /![]() , w
= 20
, w
= 20
The equation is
24
(20 - 3 /![]() )t
20 + 3 /
)t
20 + 3 /![]() t
t
y =
sin
sin
6(400 -
9/4)
2
2
Problem 5
Please
answer the following true or false. If
false, explain why or provide a counter-example.
If true, explain why.
A. If the lion population P(t) of Africa follows the differential equation
P'(t) = -10P(10,000 - P)(30,000 - P)
and there are 20,000 lions in Africa today, then
the lions will eventually become extinct in Africa.
We graph P' vs. P below
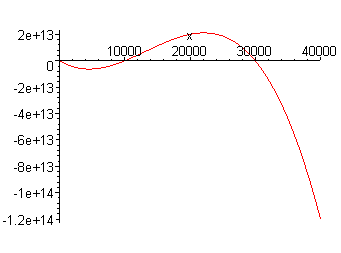
We see that 10,000 is an unstable equilibrium point and 30,000 is a stable equilibrium point. Hence if we begin with a population of 20,000, it will rise towards 30,000 and the population will not become extinct. The statement is false.
B.
(15 Points) Let f(t) = sin(t2)e10t
. Then the Laplace transform of
f(t)
is defined for all s
> 10
.
True, by the existence theorem of Laplace Transforms,
|sin(t2)e10t| < e10t
C.
(15 Points) Suppose that y1(x)
and y2(x)
are differentiable functions and y'' + p(x)y' + q(x)y = 0
is a differential equation such that p(x)
and q(x)
are continuous functions. If the Wronskian of y1(x)
and y2(x)
is
e3x
W =
1 + x2
then y1(x)
and y2(x)
cannot be solutions to the differential equation.
False, W is never zero.
D.
(15 Points) Suppose that two-dimensional system x'
= Ax
of differential equations has the phase portrait pictured below.
Then the eigenvalues of A are real
and distinct.
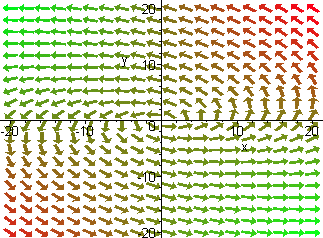
False, the origin is a spiral node. Hence the eigenvalues of A are complex.