Math 203 Practice Midterm 3

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.  Do your work on your own paper.

  Printable Key

Problem 1

A physicist has plotted the position of a projectile over time.  Based on Newton’s laws, the projectile should ideally travel in a parabolic path.  Use matrices to find the most likely equation of this parabola.  (You may use a calculator, but show the matrices that are being manipulated).

  Solution

Problem 2

A new species of fish is introduced into the Truckee River.  Initially 2 fish were stocked.  It takes one year for this species to spawn, when each fish averages 3 successful children each year.  (So there are 2 at the beginning, 2 at the end of the first year, 8 at the end of the second year, 14 at the end of the third year, etc.)

A.     Assuming no fish die, set up a recursion relationship that gives the number of fish w_n at the end of year n.

Solution

B.     Find a matrix A such that w_n-1  =  A^n-1(w₀, w₁)^T .

Solution

C.     Find a diagonal matrix D such that A is similar to D.

      Solution

Problem 3

Let V be the subspace of differentiable functions spanned by {e^x, e^2x, e^3x} and let

        L:  V --->  V

be the linear transformation with 

        L(f(x))  =  f ''(x) - 3f '(x) + 2f(x)

A.     Write down the matrix A_L with respect to the given basis.

Solution

B.     Find the a basis for the kernel and range of L.  

      Solution

Problem 4 

Let W = Span{(1,1,0,1), (0,1,2,3)}.  Find a basis for the orthogonal complement of W.

      Solution

Problem 5

Let 

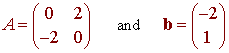
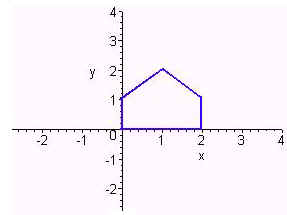
and T be the affine transformation T(x)  =  Ax + b .  Sketch the image under T of the figure below.

          Solution

Problem 6

Let  L:  V ---> V  be a linear transformation.  Use the fact that 

        dim(Ker L) + dim(Range L)  =  dim(V)

to show that if L is one to one then L is onto. 

          Solution

Problem 7 

Let A and B be matrices and let v be an eigenvector of both A and B.  Prove that v is an eigenvector of the product AB.

         Solution

Problem 8

Answer True of False and explain your reasoning.

A.    Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors.  Then

        Solution

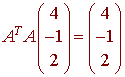
B.     Let V be the vector space of continuous functions then the expression

        <f, g>  =  f(1) + g(1)

defines an inner product on V.

        Solution