Math 203 Practice Midterm 3
Please work out each
of the given problems. Credit will
be based on the steps towards the final answer.
Show your work. Do your work
on your own paper.
A physicist has plotted
the position of a projectile over time. Based
on Newton’s laws, the projectile should ideally travel in a parabolic path.
Use matrices to find the most likely equation of this parabola.
(You may use a calculator, but show the matrices that are being
manipulated).
|
Time |
1 |
2 |
3 |
4 |
|
Distance |
2 |
30 |
20 |
2 |
Solution
We consider the matrix and vector
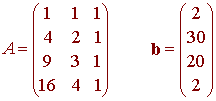
Then we solve the system
ATAx = ATb
which becomes
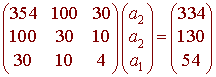
We now rref the corresponding augmented matrix
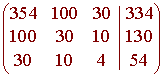
to get
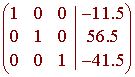
We can conclude that the least squares regression parabola is given by
y = -11.5x2 + 56.5x - 41.5
A
new species of fish is introduced into the Truckee River.
Initially 2 fish were stocked.
It takes one year for this species to spawn, when each fish averages 3
successful children each year. (So
there are 2 at the beginning, 2
at the end of the first year, 8 at the end of the
second year, 14 at the end of the third year, etc.)
A.
Assuming no fish die, set up a recursion relationship that gives the
number of fish wn
at the end of year n.
We have that the number of fish should be the number previous plus the offspring of those two years ago. We get
wn = wn-1 + 3wn-2
wn-1 = wn-1
B.
Find a matrix A such that wn-1
= An-1
(w0, w1)T
.
We can write the recursive equation as
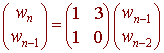
The above 2 x 2 matrix is what is required.
C.
Find
a
diagonal matrix D such that A
is similar to D.
Solution
We need to find the eigenvalues and eigenvectors for A. First for the eigenvalues. We have
det(A - lI) = (1 - l)(-l) - 3 = l2 - l - 3 = 0
has roots
![]()
The diagonalized matrix is
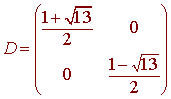
Let
V be the subspace of differentiable functions
spanned by {ex, e2x, e3x}
and let
L: V
---> V
be the linear transformation with
L(f(x)) = f ''(x) - 3f '(x) + 2f(x)
A.
Write down the matrix AL with
respect to the given basis.
We have
L((1,0,0) = L(ex) = ex - 3ex + 2ex = 0 = (0,0,0)
L((0,1,0) = L(e2x) = 4e2x - 6e2x + 2e2x = 0 = (0,0,0)
L((0,0,1) = L(e3x) = 9e3x - 9e3x + 2e3x = 2e3x = (0,0,2)
The matrix of L is the matrix whose columns are the vectors above.
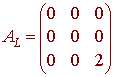
B.
Find the a basis for the kernel and range of L.
A basis for the kernel corresponds to the null space of AL which has basis
{(1,0,0), (0,1,0)}
in other words the basis is given by
{ex, e2x}
Problem 4
Let W
= Span{(1,1,0,1), (0,1,2,3)}. Find
a basis for the orthogonal complement of W.
The orthogonal complement is equal to the null space of the matrix whose rows are the given vectors. If
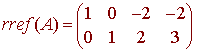
then the rref(A) is given by
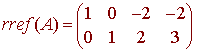
so that a basis for the null space is given by
{(2,-2,1,0), (2,-3,0,1)}
Problem 5
Let
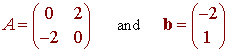
and T
be the affine transformation T(x) = Ax + b
. Sketch the image under T
of the figure below.
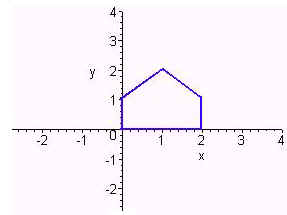
We just compute T(x) for each of the vertices and use the theorem that under an affine transformation line segments go to line segments. We have
T(0,0) = (0,0) + (-2,1) = (-2,1) T(2,0) = (0,-4) + (-2,1) = (-2,-3)
T(2,1) = (2,-4) + (-2,1) = (0,-3) T(1,2) = (4,-2) + (-2,1) = (2,-1)
T(0,1) = (2,0) + (-2,1) = (0,1)
The image is shown below in red. Notice that this is a rotation by -p/2 then a expansion by a factor of 2 then a translation by (-2,1)
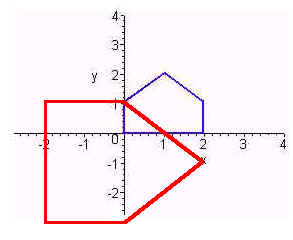
Problem 6
Let L: V ---> V be a linear transformation. Use the fact that
dim(Ker L) + dim(Range L) = dim(V)
to show that if L
is one to one then L is onto.
Solution
dim(Ker L) = 0
The equation tells us that
dim(Range L) = dim(V)
Since the range is a subspace of V and has the same dimension as V, the range of L equal V. We can conclude that L is onto.
Problem 7
Let A
and B be matrices and let v
be an eigenvector of both A and B.
Prove that v
is an eigenvector of the product AB.
Proof
Av = av and Bv = bv
We then have
(AB)v = A(Bv) = A(bv) = b(Av) = bav = abv
Hence v is an eigenvector of AB with eigenvalue ab.
Problem 8
Answer True of False and
explain your reasoning.
A. Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors. Then
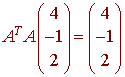
Solution
True, since A is an orthogonal matrix, we have
AT = A-1
so that
ATA = A-1A = I
B. Let V be the vector space of continuous functions then the expression
<f, g> = f(1) + g(1)
defines an inner product on V.
SolutionFalse, for example if
f(x) = -x
then
<f, f> = f(-1) + f(-1) = -1 + -1 = -2 < 0
violating the first property of inner products.