Practice Exam III

Key

Problem 1  Graph the inequality.

        2x - 5y  > 10

Problem 2  Perform the indicated operations.

A.  (3v⁴ - 5v³ + 9v - 1)  +  (2v⁴ + 7v² - 8v - 3)

B.  (2x⁵ - x⁴ - 5x³ + 3x² - 6)  -  (4x⁵ - x⁴ - 2x³ + 3x² - 7x - 10)

Problem 3  Find each product

A.  3x⁸yz²(5xy² + 3x³z² - 6y + 1)

B.  (2x - 3)(x³ + 4x - 10)

Problem 4  Find each product

A.  (2x + 9)(3x - 1)

B.  (3x - 1/2)(4x - 2/3)

C.  (x + 1)(x + 2)(x + 3)

Problem 5  Use the special product formulas to find

A.  (3x - 4)²

B.  (7z - 3)(7z + 3)

Problem 6  Simplify

A.  (x²y⁵x⁴)¹⁰

B.       -20(a²b)⁷ 
                            
          (2ab⁵)²a⁵

Problem 7  Simplify and write without negative exponents.

        (x ^-3 y) ^-2(x ^-4)

Problem 8  The Milky Way galaxy is about 120,000 light years across.  One light year is 950,000,000,000,000 meters long.

A.  Write both of these numbers in scientific notation.

B.  How many meters wide is the milky way galaxy?  Write your answer in scientific notation.

Problem 9  Solve each compound inequality.  Write the solution set using interval notation and graph it.

A.  x - 4 > 1   or    7 - x  > 5

B.  2/3 x  < 4   and   x - 5  > 4

Problem 10  Solve the absolute value inequality and graph the solution set.

A.  3|2 - x| + 5  >  14

B.  5|6 - x| +7  >  3

Problem 11  Find the domain and range of each relation.  Then determine whether it is a function.

A.  {(1,2), (2,4), (4,7), (4,8)}

B.  x + 6y  = 12

C.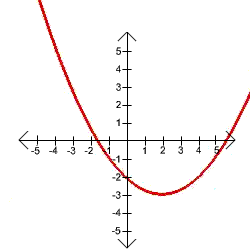   

Problem 12  Let

    f(x) = 3x - 5     and     g(x)  =  x² - x

Find

A.  (f + g)(x)

B.  (f - g)(3)

e-mail Questions and Suggestions