Practice Exam III
Problem 1 Graph the inequality.
2x - 5y > 10
Solution
First find the intercepts of the line:
First, when x = 0 we get
-5y = 10
Divided both sides by -5 to get
y = -2
Next, when y = 0 we get
2x = 10
Divide both sides by 2 to get
x = 5
In T-table form, this gives
| x | y |
| 0 | -2 |
| 5 | 0 |
so we get the two points
(0,-2) and (5,0)
Now plot the two points and connect with a dashed line as shown below:
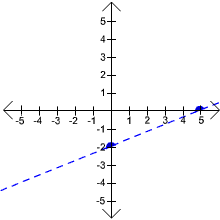
Now test the origin (0,0):
2(0) - 5(0) = 0 > 10
is a false statement, so we shade in the part of he plane that is away from the origin. The solution is shown below:
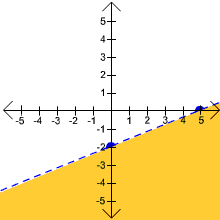
Problem 2 Perform the indicated operations.
A. (3v4 - 5v3 + 9v - 1) + (2v4 + 7v2 - 8v - 3)
Solution
We just combine like terms. Notice that we can drop the parentheses, since we are adding:
3v4 - 5v3 + 9v - 1 + 2v4 + 7v2 - 8v - 3
= 3v4 + 2v4 - 5v3 + 7v2 + 9v - 8v - 1 - 3
= 5v4 - 5v3 + 7v2 + v - 4
B. (2x5 - x4 - 5x3 + 3x2 - 6) - (4x5 - x4 - 2x3 + 3x2 - 7x - 10)
Solution
We first distribute the "-" through by changing all of the signs of the second expression
= 2x5 - x4 - 5x3 + 3x2 - 6 - 4x5 + x4 + 2x3 - 3x2 + 7x + 10
Now combine like terms
= 2x5 - 4x5 - x4 + x4 - 5x3 + 2x3 + 3x2 - 3x2 + 7x - 6 + 10
= -2x5 - 3x3 + 7x + 4
Problem 3 Find each product
A. 3x8yz2(5xy2 + 3x3z2 - 6y + 1)
Solution
We use the distributive property (multiply through) and use the product rule for exponents:
= 15x8+1 y1+2 z2 + 9x8+3 y z2+2 - 18x8y1+1z2 + 3x8yz2
= 15x9y3z2 + 9x11yz4 - 6x8y2z2 + 3x8yz2
B. (2x - 3)(x3 + 4x - 10)
Solution
Use the distributive law. First with the 2x and then with the -3:
= 2x(x3 + 4x - 10) + (-3)(x3 + 4x - 10)
= 2x4 + 8x2 - 20x - 3x3 - 12x + 30
Now combine like terms
= 2x4 - 3x3 + 8x2 - 20x - 12x + 30
= 2x4 - 3x3 + 8x2 - 32x + 30
Problem 4 Find each product
A. (2x + 9)(3x - 1)
Solution
Use FOIL
= (2x)(3x) + (2x)(-1) + (9)(3x) + (9)(-1)
= 6x2 - 2x + 27x - 9
Now combine like terms
= 6x2 + 25x - 9
B. (3x - 1/2)(4x - 2/3)
Solution
Use FOIL
= (3x)(4x) + (3x)(-2/3) + (-1/2)(4x) + (-1/2)(-2/3)
= 12x2 - 2x - 2x + 1/3
Now combine like terms
= 12x2 - 4x + 1/3
C. (x + 1)(x + 2)(x + 3)
Solution
Use FOIL on the first two factors
(x + 1)(x + 2) = x2 + 2x + x + 2 = x2 + 3x + 2
Now multiply this by the third term
(x + 3)(x2 + 3x + 2) = (x)(x2 + 3x + 2) + 3(x2 + 3x + 2)
= x3 + 3x2 + 2x + 3x2 + 9x + 6
Now combine like terms
= x3 + 6x2 + 11x + 6
Problem 5 Use the special product formulas to find
A. (3x - 4)2
Solution
This is the square of a binomial. We have
(3x)2 + 2(3x)(-4) + (-4)2
= 9x2 = 24x + 16
B. (7z - 3)(7z + 3)
Solution
This is the difference of squares. We have
= (7z)2 - (3)2
= 49z2 - 9
Problem 6 Simplify
A. (x2y5x4)10
Solution
First use the product rule on the x's.
= (x2+4y5)10 = (x6y5)10
Use the power rule.
= x(6)(10)y(5)(10)
= x60y50
B. -20(a2b)7
(2ab5)2a5
Solution
First use the power rule (multiply the 7 through the top and the 2 through the bottom.)
-20a14b7
=
4a2b10a5
Now use the product rule on the a's.
-20a14b7
=
4a7b10
Now use the quotient rule.
-5a7
=
b3
Problem 7 Simplify and write without negative exponents.
(x -3 y) -2(x -4)
Solution
First use the power rule
= (x6 y-2)(x -4)
Now use the product rule
= x2 y-2
Now remember that we can write without negative exponents.
x2
=
y2
Problem 8 The Milky Way galaxy is about 120,000 light years across. One light year is 950,000,000,000,000 meters long.
A. Write both of these numbers in scientific notation.
Solution
The first number is
1.2 x 105
and the second number is
9.5 x 1014
B. How many meters wide is the milky way galaxy? Write your answer in scientific notation.
Solution
We just multiply the two numbers.
(1.2 x 105)(9.5 x 1014) = (1.2)(9.5)(105)(1014)
= 11.4 x 1019 = 1.14 x 101 x 1019 = 1.14 x 1020
Problem 9 Solve each compound inequality. Write the solution set using interval notation and graph it.
A. x - 4 > 1 or 7 - x > 5
Solution
We add 4 to both sides of the first inequality and -7 to both sides of the second.
x > 5 or -x > -2
Now multiply both sides of the second inequality, remembering to switch the inequality sign
x > 5 or x < 2
In interval notation we get
(-
![]() , 2)
U (5,
, 2)
U (5,
![]() )
)
Now put this on a number line
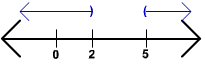
B. 2/3 x < 4 and x - 5 > 4
Solution
Multiply the both sides of the first by 3/2 and add 5 to both sides of the second to get
x < 6 and x > 9
Notice that these cannot happen simultaneously, so the solution is the empty set.
Problem 10 Solve the absolute value inequality and graph the solution set.
A. 3|2 - x| + 5 > 14
Solution
First subtract 5 from both sides to get
3|2 - x| > 9
Then divide both sides by 3 to get
|2 - x| > 3
Now turn it into an or statement to find the endpoints
2 - x = 3 or 2 - x = -3
Subtract 2 from both sides to get
-x = 1 or -x = -5
Now multiply both sides by -1 to get
x = -1 or x = 5
Now check test points. First if x = -2, the equation gives
3|-2 - 2| + 5 = 3|-4| + 5 = 3(4) + 5 = 12 + 5 = 17
which is greater than 14, so the region to the left of -1 is included. Now test x = 0.
3|0 - 2| + 5 = 3|-2| + 5 = 3(2) + 5 = 6 + 5 = 11
which is not greater than 14, so the middle region is not included. Finally test x = 6 to get
3|6 - 2| + 5 = 3|4| + 5 = 3(4) + 5 = 12 + 5 = 17
which is greater than 14, so the region to the right of -1 is included. In interval notation, we get
(-
![]() , -1)
U (5,
, -1)
U (5,
![]() )
)
The graph is shown below
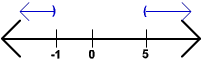
B. 5|6 - x| +7 > 3
Solution
First subtract 7 from both sides to get
5|6 - x| > -4
Then divide both sides by 5 to get
|6 - x| > -4/3
Now notice that the right hand side is negative. The absolute value if always greater than a negative number, so the solution is all real numbers.
Problem 11 Find the domain and range of each relation. Then determine whether it is a function.
A. {(1,2), (2,4), (4,7), (4,8)}
Solution
The domain is the set of first coordinates:
{1,2,4}
and the range is the set of second coordinates:
{2,4,7,8}
Since the number 4 gets sent to both 7 and 8, this is not a function.
B. x + 6y = 12
Solution
This is the equation of a line. Notice that the slope is defined:
6y = -x + 12
y = -1/6 x + 2
Since the slope is defined, the line is not vertical, hence the graph passes the vertical line test, and the equation is a function.
C. 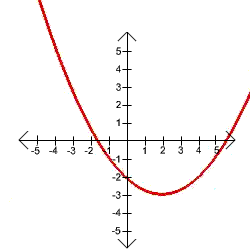
Solution
This graph passes the Vertical Line Test, since every vertical line passes through the graph at most once, hence it is the graph of a function.
Problem 12 Let
f(x) = 3x - 5 and g(x) = x2 - x
Find
A. (f + g)(x)
Solution
Just add
(3x - 5) + (x2 - x)
= 3x - 5 + x2 - x
Now combine like terms and put in descending order to get
= x2 + 2x - 5
B. (f - g)(3)
Solution
Subtract to get
(3x - 5) - (x2 - x)
Now multiply the "-" through to get
3x - 5 - x2 + x
Now combine like terms and put into descending order to get
-x2 + 4x - 5
e-mail Questions and Suggestions