Math 117 Practice Midterm 3
Please work out each of the given problems. Credit will be based on the steps that you show towards the final solution. Show your work.
Problem 1
Solve the differential Equation
xy' - 2x = x2 y(1) = 5
Solution
Problem 2
Determine if
1
y = cos t -
e-t cos t
5
is a solution to the differential equation
y''' - y'' + y' - y = e-t sin t
Problem 3
The rate of growth in customers for a small business is proportional to the product of the number of customers who eat at the restaurant divided by the total number of years that the restaurant has been in business. After one year in business the restaurant averages 20 customers per day, and after two years in business the restaurant averages 25 customers per day. Approximately how many customers can the restaurant expect to have per day after three years in business?
Problem 4
Use the sixth degree Taylor polynomial for
f(x) = 2 cos x
to approximate
![]() . Hint:
Use the fact that
. Hint:
Use the fact that
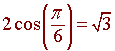
Problem 5
Find the Taylor series center at x = c for the given function and find its radius of convergence.
x2f(x) =
1 + x3
Problem 6
Use Newton's Method to approximate the intersection of the curves
y = sin x and y = 1 - x