Math 117 Practice Midterm 3
Please work out each of the given problems. Credit will be based on the steps that you show towards the final solution. Show your work.
Problem 1
Solve the differential Equation
xy' - 2x = x2 y(1) = 5
Solve for y':
xy' = 2x + x2
y' = 2 + x
Now integrate to get
x2
y = 2x +
+ C
2
Problem 2
Determine if
1
y = cos t -
e-t cos t
5
is a solution to the differential equation
y''' - y'' + y' - y = e-t sin t
We take three derivative of y:
1
y' = -sin t +
(e-t cos t + e-t sin t)
5
1
y'' = -cos t +
(-e-t cos t - e-t sin t - e-t
sin t + e-t cos t )
5
1
= -cos t -
(2e-t sin t )
5
2
y''' = sin t +
(e-t sin t - e-t cos t)
5
Now plug the these derivatives into the differential equation:
2
1
sin t +
(e-t sin t - e-t cos t) + cos t +
(2e-t sin t)
5
5
1
1
- sin t +
(e-t cos t + e-t sin t) - cos t +
e-t cos t
5
5
2e-t sin t - 2e-t cos t + 2e-t sin t + e-t cos
t + e-t sin t + e-t cos t
=
5
5e-t sin t
=
= e-t sin t
5
Problem 3
The rate of growth in customers for a small business is proportional to the product of the number of customers who eat at the restaurant divided by the total number of years that the restaurant has been in business. After one year in business the restaurant averages 20 customers per day, and after two years in business the restaurant averages 25 customers per day. Approximately how many customers can the restaurant expect to have per day after three years in business?
We write the differential equation
dx
kx
=
dt
t
Separating the variables gives
dx
kdt
=
x
t
Now integrate both sides to get
ln x = k ln t + C
When t = 1, x = 20 so that
ln 20 = k ln 1 + C = C
When t = 2, x = 25 so that
ln 25 = k ln 2 + ln 20
k ln 2 = ln 25 - ln 20 = ln 1.25
so that
ln 1.25
k =
= 0.322
ln 2
We have
ln x = 0.322 ln t + ln 20
Plugging in 3 for t gives
ln x = 0.322 ln 3 + ln 20 = 3.35
Exponentiating both sides gives
x = e3.35 = 29
We conclude that there will be 29 customers per day in three years.
Problem 4
Use the sixth degree Taylor polynomial for
f(x) = 2 cos x
to approximate
![]() . Hint:
Use the fact that
. Hint:
Use the fact that
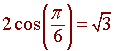
We find the first six derivatives of f and evaluate them at 0
f(0) = 2 cos 0 = 2
f '(0) = -2 sin 0 = 0
f ''(0) = -2 cos 0 = -2
f '''(0) = 2 sin 0 = 0
f (iv)(0) = 2 cos 0 = 2
f iv)(0) = -2 sin 0 = 0
f (vi)(0) = -2 cos 0 = -2
Plugging it into the Taylor polynomial formula gives
-2
2
-2
2 cos x = 2
+
x2 +
x4 +
x6
2!
4!
6!
1
1
= 2 - x2
+
x4 -
x6
12
360
Now plug in p/6 to get
1.73205
Problem 5
Find the Taylor series center at x = c for the given function and find its radius of convergence.
x2f(x) =
1 + x3
We know that
![]()
![]()
We can write f(x) as
1
x2
1 - (-x3)
so
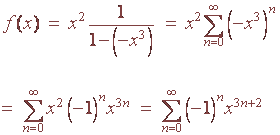
Problem 6
Use Newton's Method to approximate the intersection of the curves
y = sin x and y = 1 - x
We find the root of the difference
f(x) = sin x - (1 - x) = x - 1 + sin x
We find
f '(x) = 1 + cos x
and find
f (x)
N(x)
= x -
f '(x)
x - 1 + sin x
N(x)
= x -
1 + cos x
Now our first guess is 0,
N(0) = 2 N(2) = 0.5
N(0.5) = 0.51095795 N(0.51095795) = 0.51097343
N(0.51097343) = 0.51097343
Hence the root occurs at x = 0.51097343