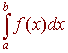Numerical Integration

 

Trapezoidal Rule

As we saw before, often we can not evaluate a definite integral because it is too difficult or because we do not have an algebraic expression for the integrand.  We saw that the Midpoint estimate was one way to approximate a definite integral.  In this section, we seek estimates that are likely to be more accurate.  The Midpoint estimate involved using rectangles to approximate the region.  Now we will play with other geometric shapes that can approximate the region.  Our first investigation will involve trapezoids.  

The trapezoidal rule which geometrically calculates the area of the trapezoid with base on the x-axis and heights f(xi) and f(xi+1) 

               

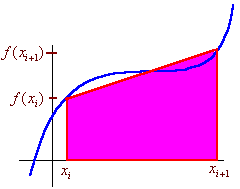
The area of the trapezoid is 

          

or the base times the average of the heights.  Adding up all the trapezoids gives


The Trapezoidal Rule

              b - a 
T(n)  =             [f(x0) + 2f(x1) + 2f(x2) +...+ 2f(xn-1) + f(xn)]
               2n

 

Example

 Use the Trapezoidal Approximation with n  =  3 to approximate the integral

               

 

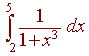
Solution

We have

        n  =  3        a  =  2        b  =  5

So 

                    b - a          5 - 2
        Dx  =               =              =  1
                       n               3

We set up a table beginning at a  =  2 incrementing Dx  = 1 and stopping at b  =  5

 
x 2 3 4 5
f(x) 1/9  =  0.1111 1/28  =  0.0357 1/65  =  0.0154 1/126  =  0.0079

 

Plug these numbers into the trapezoidal formula to get

        1/2 [0.1111 + 2(0.0357) + 2(0.0154) + 0.0079)]

        =  0.1106

The true answer is closer to .0992.  Hence the error in the approximation is 

        Error  =  0.1106 - 0.0992  =  0.0114

 

Simpson's Rule

We have just seen that a trapezoid is a pretty good approximation to an integral.  Might there be a better approximation?  It turns out that using parabolas to approximate an integral is often better than using trapezoids.  The use of parabolas to approximate an integral is called Simpson's Rule.   We will not work out the details at how to arrive at the clean formula.  We will instead just present the formula and leave it to more advanced courses to derive it.

 

Simpson's Rule

Let f(x) be a function defined on [a,b].  Then 

          S(n) = 1/3 T(n) + 2/3 M(n)

where T(n) and M(n) are the Trapezoidal and Midpoint Estimates.  S(n) is called Simpson's Estimate for the integral



There is a way of using Simpson's Rule without having to first find both the Trapezoidal and Midpoint approximations.  Just remember the pattern

        1 4 2 4 2 4 ... 2 4 2 4 1 

pattern.  Again we will not go into the derivation of the formula which can only be used for even numbers n.

 

Simpson's Rule

                    b - a
      S(n)  =              [ f(x0) + 4f(x1) + 2f(x2) + 4f(x3) + ... + 4f(xn-1) + f(xn) ]
                     3n

 



Example

Approximate 

       

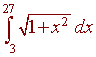
Using Simpson's Rule with n  =  6.

Solution

We have 

        n  =  6        a  =  3        b  =  27

so

          b - a
                      =  4/3
            3n

Now create a table beginning with a  =  3, incrementing by Dx  =  4, and ending at 27.

 
x 3 7 11 15 19 23 27

f(x)

 3.16 7.07 11.05 15.03 19.03 23.02 27.02

 
Finally plug these numbers into the Simpson's Rule formula

        4/3 [ 3.16 + 4(7.07) + 2(11.05) + 4(15.03) + 2(19.03) + 4(23.02) + 27.02 ]

        =  361.09

It is a remarkable fact that the true answer is close to 361.091938.  Simpson's estimate is very accurate indeed.

 

Error

We keep mentioning how accurate the various estimates are.  However, usually the exact answers are unavailable (if they were why would you need to use an approximation?)  Our next goal is to find a bound for the error without knowing the true value of the integral.  Once again formulas for this are available, but the derivations of the the formulas are beyond the scope of this course.  The formulas are a bit messy, but with practice, their use can be mastered.  Recall that the error is defined as the difference between the exact value and the calculated value.

 

Error Estimates for Trapezoidal and Simpson's Rules

Let ET and ES be the errors in approximating 

         

Using the Trapezoidal Rule and Simpson's Rule respectively.  Then 

                          (b - a)3
            |ET|  <                Max[f ''(x)]         for    a  <  x  <  b
                          12n2

 

                         (b - a)5
            |ES|  <                Max[f ''''(x)]         for    a  <  x  <  b
                        180n4

 

Looking at these formulas, we should ask ourselves which approximation gives a more accurate result.  Typically the work of approximating an integral is performed with a calculator or computer, where the values of n are very large.  Since the error estimate for Simpson's Rule has an n4 in the denominator, while the error estimate for the Trapezoidal rule has an n2 in the denominator, Simpson's Rule will produce a more accurate estimate for large n.

 

Example

ln(2) can be estimated by integrating 

       

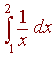
If n  =  1000, how accurate will each of the approximations be?

 

Solution

We have

        n  =  1000      a  =  1         b  =  2

Now calculate the derivatives

        f '(x)  =  -x -2         f ''(x)  =  2x -3         f '''(x)  =  -6x -4         f ''''(x)  =  24x -5 

The absolute values of both f ''(x) and f ''''(x) are decreasing functions between x  =  1 and x  =  2, hence their maximums occur at the left most value of x, namely x  =  1.  We have

        |f ''(1)|  =  2        and        |f ''''(1)|  =  24

Now we can plug the numbers into the error estimate formulas.  We have

                        (2 - 1)3
        ET   <                      (2)  =  .00000017
                     12(1000)2

                       (2 - 1)5
        ES   <                      (24)  =  .00000000000013
                    180(1000)4

It is clear the both estimates have very little error, however Simpson's has a much smaller error.

You can find a nice demonstration of the approximation at http://math.furman.edu/~dcs/java/NumericalIntegration.html

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions