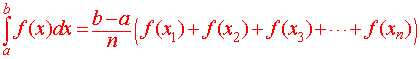Riemann Sums

Using the Midpoint Rule to Approximate Area Under a Curve (an Example)

What if we wanted to paint a wall that has a ceiling the shape of 

            50
y  =                     
         10 +  x²  

a flat floor and a right wall at x = 1 yards and a left wall at x = 4 yards.  We could try to use the fundamental theorem of calculus, but we would hit a major stumbling block when trying to find an antiderivative.  Since we are just painting a wall, not performing open heart surgery, we only need an approximation. 

We can approximate the area by cutting out 6 rectangles.  Since the base of the wall is 

        base of the wall  =  5 - 2

and there are 6 rectangles, the base of each rectangle is 

                                                 5 - 2
        Base of each rectangle  =             = .5 yards
                                                   6

The height of each rectangle is the y-coordinate of the midpoint of each rectangle.  The x- coordinates are can be found by starting with the x- coordinate of the first midpoint, 1.25, and then adding the base, .5, times the rectangle number starting at 0.

        1.25 + 0(.5)            1.25 + 1(.5)             1.25 + 2(.5)     

        1.25 + 3(.5)          1.25 + 4(.5)           125 + 5(.5) 

so that the y coordinates are

                     50                                        50                                  50
                                          ,                                         ,                                        
         10 +  (1.25 + 0(.5))²             10 +  (1.25 + 1(.5))²          10 +  (1.25 + 2(.5))² 

                     50                                        50                                      50
                                          ,                                             ,                                          
         10 +  (1.25 + 3(.5))²           10 +  (1.25 + 4(.5))²            10 +  1.25 + 5(.5))²

Simplified values of these expressions are

 

x	1.25	1.75	2.25	2.75	3.25	3.75
y	4.3243	3.8278	3.3195	2.8470	2.4316	2.0779

To get the area of the each rectangle we multiply the height by the base.  Since the base is 0.5 for all of the rectangles, we just multiply the y coordinates by 0.5

 

Rectangle	1	2	3	4	5	6
Area	2.1622	1.9139	1.6598	1.4235	1.2158	1.039

Finally to get the total area we add the terms up:

        2.1622 + 1.9139 + 1.6598 + 1.4235 + 1.2158 + 1.039  =  9.4142

The area of the wall is approximately 9.4142 square yards.  

By the way, the first 6 significant digits of the exact area is 9.41655 square yards.  For this example, we were off by less than 0.003 square yards.  A small enough error to still order the right amount of paint.

The Midpoint Rule (Formula)

The process that was used to approximate an area can be used for any region.  We have the option of choosing more or fewer than 6 rectangles and the bounds can be any numbers.  In general

Exercise

Approximate

Using the midpoint approximation with three rectangles.

Hold your mouse on the yellow rectangle for the answer. 

Example  

Use the midpoint rule with four rectangles to approximate the area of the pond pictured below.  Numbers are listed in meters.

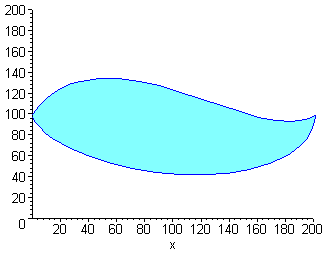
Solution

To approximate this volume we cut the interval [0,200] into four equal pieces.

        [0,50]      [50,100]     [100,150]     and     [150,200]

Then sketch the four rectangles with verticals coming from the midpoints as in the picture below.

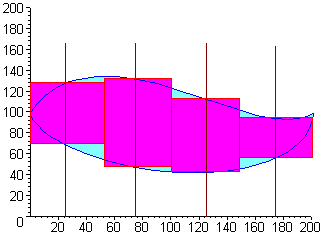
The sum of the areas of the four rectangles will be the approximate area of the pond.  We can eyeball the heights of the four rectangles as 60, 85, 72, and 40.  We can use the midpoint formula

                        200 - 0
        Area  @                    (60 + 85 + 72 + 40)  =  12,050
                             4        

The area of the pond is approximately 12,050 square meters.

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions