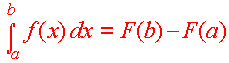The First Fundamental Theorem of Calculus

Definition of The Definite Integral

Let f(x) be a continuous positive function between a and b and consider the region below the curve y  = f(x), above the x-axis and between the vertical lines x  =  a and x  =  b as in the picture below. 

We are interested in finding the area of this region.  We first make the following definition

 

The Definite Integral Let f(x) be a continuous positive function between a and b and consider the region below the curve y  = f(x), above the x-axis and between the vertical lines x  =  a and x  =  b.  Then denote the area of this region by            and call this the definite integral of f(x) from a to b.

The First Fundamental Theorem of Calculus

The question that comes up naturally is, "What does the definite integral have to do with the antiderivative?"  The answer is not obvious, but was found by two of the greatest mathematicians of all time, Liebnitz and Newton.  Their result is called the first fundamental theorem of calculus.

   

The First Fundamental Theorem of Calculus Let F(x) be a function such that F '(x)  =  f(x) then

The proof of this theorem is too difficult for this course.  A proof can be found at http://www.ltcconline.net/greenl/courses/105/antiderivatives/FIRSTFUN.HTM

Example

Find the area under the curve y  =  x³ above the x-axis and between x  =  0 and x  =  2.

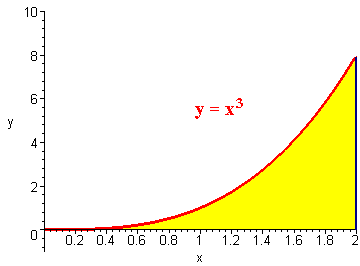
Solution

We use the first fundamental theorem of calculus to get

Notice the notation that was used.

Properties of the definite integral

Thinking of the definite integral as the area under the curve leads to some properties that we will use from time to time.  If a and b are equal, then the length of the base is zero.  The area of a figure with zero width is zero.  This leads to the first property.  Secondly, if we cut the region into two pieces, one going from a to b and the other going from b to c, then the total area is the sum of the first two areas.  This leads to the second property.  If we think of area in terms of antiderivatives, then 

        F(b) - F(a)  =  -(F(a) - F(b))

This suggests that if we go from b to a instead of from a to b, we have the same definite integral except with a negative attached.  This leads to the third property.  We state these properties now.

 

Properties of the Definite Integral

Example:

Find the area under the curve

        y  =  | x - 2 | 

between x  =  -2   and    x  =  4

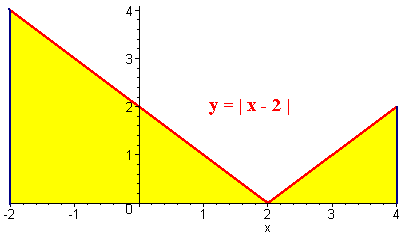
Solution 

The difficulty is that the absolute value does not have a nice antiderivative.  However, we can strip the absolute value sign if we know that x > 2 or x < 2.  We have

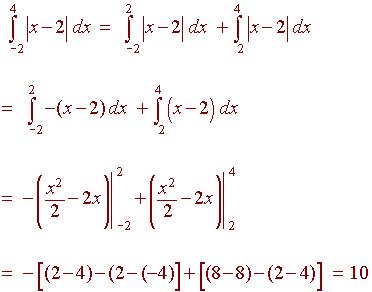
The Average Value

We think of the average as the sum over the total.  We will see later on that the definite integral is actually a sum.  The total will be b - a.  This leads us to a definition of  the average value of f(x) between a and b as

 

Average Value of a Definite Integral

Example:  

The revenue at a slot machine manufacturing company can be modeled by the equation

        R(x)  =  50x - 20

find the average revenue for the first 100 units sold.

Solution

We compute 

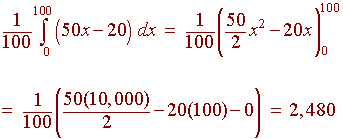
The average revenue is $2,480 per machine.

Back to the Math 116 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions