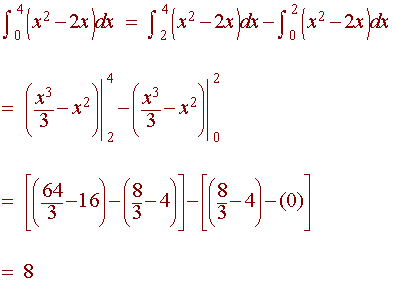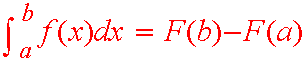The First Fundamental Theorem of Calculus
The First Fundamental Theorem of Calculus:
Statement and Proof
| The First Fundamental Theorem of Calculus
Let f be a continuous function on
[a,b] and let
|
Proof:
Cut up the interval [a,b] into several pieces with
a = x0 < x1 < x2 < x3 < ... < xn-1 < xn = b
Then
F(b)
- F(a) =
[F(xn) - F(xn-1)] + [F(xn-1) - F(xn-2)]
+ [F(xn-2) - F(xn-3)] +... + [F(x2) - F(x1)]
+ [F(x1) - F(x0)]
=
![]()
By the mean value theorem there is a ci between xi-1 and xi with
F(xi) - F(xi-1)
F(xi) - F(xi-1)
F'(ci)
=
=
xi - xi-1
Dxi
Multiplying both sides by Dxi gives
F'(ci)Dxi = F(xi) - F(xi-1)
Substituting into the sum gives
![]()
Taking
the limit as n approaches infinity, gives the definite integral.
Examples
Example 1:
![]()
Example 2:
Find the area bounded by the curve
y = x2 - x , y = 0, x = 4
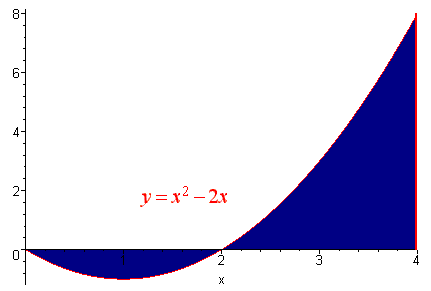
Notice that there is area both below the x-axis and above. We can find: