Amortized Loans
Section 5.4
Amortized Loan: A loan for which the loan amount plus interest owed is paid off in a series of regular equal payments.
Previously, add-on interest loans were a type of amortized loans.
The difference is the amount of interest paid.
An amortized loan can be viewed as the FV of an ordinary annuity.
FV (annuity) = FV (amortized loan)
![]()
Example 1:
What is a better deal? Borrowing $5000 for one year @ 10% simple interest amortized or add-on interest? What is the monthly payment of each?
Simple interest Amortized:
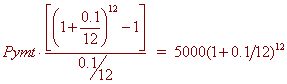
pymt = $439.58
Add-on Loan:
pymt
= FV
= $5000(1 +
(0.1)(1))
# of pymts 12
= $5500/12 = $458.33
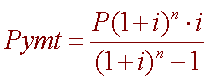 |
The better deal is the amortized loan.
Why are the payments less with an amortized loan? The add-on interest loan calculates interest on the initial amount $5000 for the entire length of the loan. The simple interest amortized loan calculates interest on the balance of the loan after each payment so the interest decreases.
Example 2:
Set up amortization table for the 1st three months of payments for the better deal. We know the payments are $439.58.
1st payment: I = Prt
$5000(.1)(1/12) = $41.67 interest
$439.58 – 41.67 = $397.91 Principal paid
$5000 – 397.91 = $4602.09 new balance
Finding unpaid balance:
Current value of loan – Current value of annuity
Unpaid Balance = P(1 + i)n
- Pymt(1 + i)n – 1
i
In this case n represents the number of payments already made.
Example 3:
Find the unpaid balance on the loan in EX 2 after 6 months.
n = 6
Unpaid balance = $5000(1 + .1/12)6 - $439.58(1
+ .1/12)6
.1/12
Owe:
$5255.27 – $2693.04 = $2562.23
How much do you save by paying off early? If we continue to make payments
6(439.58) = $2637.48 – 2562.23 = $75.28 interest
Review for Exam #1
Dimensional Analysis: Converting units of measurement
6.1
Perimeter (Circumference of Circles) and Area: One-dimensional and two-dimensional measurements of figures; Quadrilaterals, Triangles, Circles.
6.5
Right Triangle Trigonometry: Special Triangles; 45*, 30-60-90*.
Trig Ratios: Sine, Cosine, Tangent.
Finding angle q by Arcsine, Arccosine, Arctangent
5.1
Simple Interest and Future Value (FV) Add-on Interest, Finance charges,
Average Daily Balance (ADB)
5.2
Compound Interest and FV
Annual Yield, Periodic Rate
5.3
Annuities and FV, Payment Period, Term,
Ordinary Annuity , Tax-Deferred Annuity (TDA)
5.4
Back to Finance, Geometry and Logic Main Page
Back to the Survey of Math Ideas Home Page