Solving an Ellipse
Below is a picture that relates the foci, eccentricity, and length of the major and minor axes.
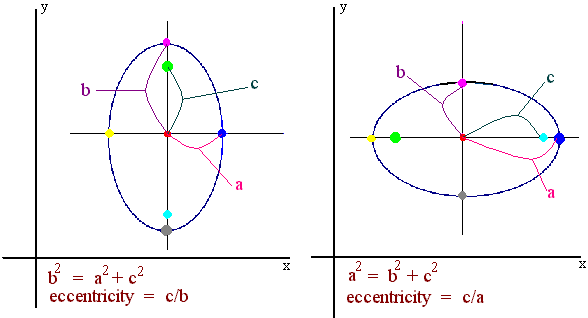
We can derive the identities if we recall that if P is a point on the ellipse the sum of the distances from P to the two foci is a constant. We will derive the equation for the ellipse with vertical major axis. The derivative for the horizontal major axis case is similar.
First consider the top of the ellipse. The sum of the distances from the two foci to the top of the ellipse is
(b - c) + (b + c) = 2b
The square of this sum is given by
4b2
Next consider the right side of the ellipse. Notice that the distances from each focus to the right side is the same. The square of this sum is
(2d)2 = 4d2
by the Pythagorean theorem,
d2 = a2 + c2
Substituting, and setting these equal to each other gives
4b2 = 4(a2 + c2)
so that
b2 = a2 + c2
To use the applet below follow these steps
- Click on the "New Problem"
button.
- Enter the correct number in the boxes and
hit the enter key. Enter the eccentricity as a fraction such as
2/3.
- If you need assistance, click on the "Hint" button.
Written Exercises
When you have mastered the above tutorial, please answer the following in a few complete sentences
-
If you know the center an one focus, how do you find the coordinates of the other focus?
-
How do you find the left vertex if you know the center, a focus, and the top vertex?
-
How do you find the center of an ellipse if you know the eccentricity, the left endpoint, and one focus (on the horizontal axis)?
Back to Larry Green's Applet Page