Scaled Diagrams
In this lesson, we will investigate scaled diagrams. We will be using the technique of ratios for the first example.
Example 1
The actual width of a rectangle is 20 centimeters (cm). Use the scale drawing of the rectangle to find the actual length ( l ).
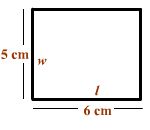
Solution
We can use the technique of ratios. In words, we can say that the length (6) of the diagram over the width (5) of the diagram is equal to the length (L) of the actual rectangle over the width (20) of the actual rectangle. The corresponding equation is
6
L
=
5
20
We can multiply both sides by 20 to get
6
L = 20 x
5
We can rewrite this as
20 6
L = x
1
5
We can cross cancel the 20 and the 5 to get
4 6
L = x
= 24
1 1
So the length is 24 cm.
Exercise 1
Try the exercise below. If you want to see the answer, put your mouse on the yellow rectangle at the bottom of the exercise.
The actual width of a rectangle is 15 centimeters (cm). Use the scale drawing of the rectangle to find the actual length ( l ).
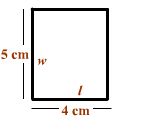
![]()
Example 2
The scale drawing of the house shown below is drawn using a scale of 1 inch (in.) = 8 feet (ft).
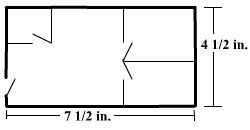
What is the length in feet of the house?
Solution
This problem asks us to convert the length 7 1/2 in. to the actual length using 1 inch = 8 feet. Notice that
2 inches = 2 x 8 feet = 16 feet
3 inches = 3 x 8 feet = 24 feet
4 inches = 4 x 8 feet = 32 feet
So to find the length we just multiply
We multiply
7 1/2 in = (7 1/2) x 8 feet
Notice that
(7 1/2)(8) = (7)(8) + (1/2)(8)
This is
= 56 feet + 4 feet = 60 ft
Exercise 2
Try the exercise below. If you want to see the answer, put your mouse on the yellow rectangle at the bottom of the exercise.
The scale drawing of the computer chip shown below is drawn using a scale of 1 centimeter (cm) = 1/2 millimeter (mm).
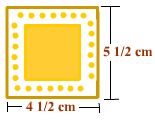
What is the length in mm of the computer chip?
![]()
Example 3
The diagram below shows a ruler (the numbers are in inches) and a map of Las Angeles County.
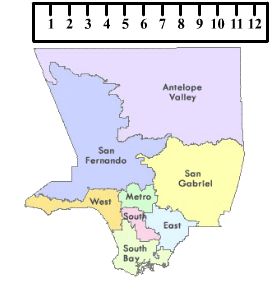
The actual distance from the west side of Antelope Valley to the east side of Antelope Valley is 55 miles. What scale was used to create the map?
Solution
We can measure this distance with the ruler and see that the distance on the map is 11 inches. We can now say that
11 inches = 55 miles
Now divide both sides by 11 to get
1 inch = 5 miles
Exercise 3
Try the exercise below. If you want to see the answer, put your mouse on the yellow rectangle at the bottom of the exercise.
Raul is using a ruler and a map to measure the distance from Brunatto to Eavesville.
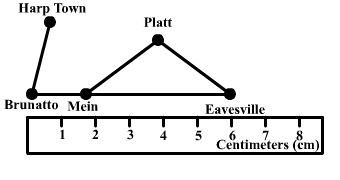
The actual distance from Brunatto to Eavesville is 48 km. What scale was used to create the map?
![]()