|
Text to Supplement Lesson on Basic Area, Perimeter and Volume In this lesson, we will review area, perimeter and volume. In particular we will first look at the definitions of basic 2-dimensional shapes: rectangles, triangles and circles and how to compute the area and perimeter of that shape. Next we will work out a problem similar to the type you may expect to see on the CAHSEE. Finally we will review how to find the volume of a rectangular solid.
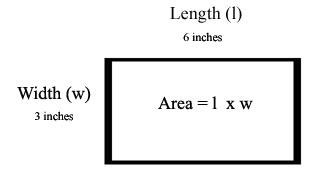
Definition: A polygon is a closed shape bounded only by straight lines. A rectangle is a 4-sided polygon in with all four of its angles are right angles.
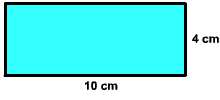
To calculate the area of a rectangle multiply its length and width together. In the above example multiply 3 inches by 6 inches Area = (3 inches)(6 inches) = 18 inches2 When computing area our answer is always given in square units. This is because pictorially what we are doing when we calculate area is equivalent to dividing up the shape into equal unit squares and adding them up. Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear. Exercise 1 Find the area of the rectangle shown below
Answer:
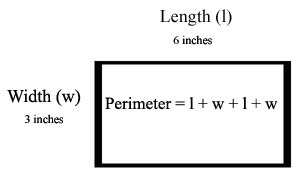
The perimeter of a polygon is equal to the distance all the way around the figure. So to calculate the perimeter of a square add twice the length and twice the width together.
The perimeter of the above rectangle is Perimeter = 12 inches + 6 inches = 18 inches. On the CAHSEE you might be asked a question about a square. Remember that a square is a rectangle in which the length and width are the same length. In this case you only need to know one side length in order to calculate both the area and the perimeter of the square.
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
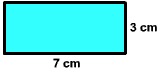
Exercise 2 Find the perimeter of the rectangle shown below
Answer:
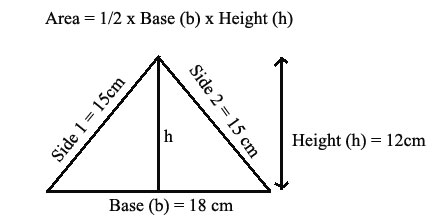
2. Finding the Area and Perimeter of a Triangle Definition: A polygon is a closed shape bounded only by straight lines. A triangle is a 3-sided polygon.
To calculate the area of a triangle multiply its base times its height and divide by two. The triangle above has area Area = 18 cm x 12 cm x (1/2) = 108 cm2
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
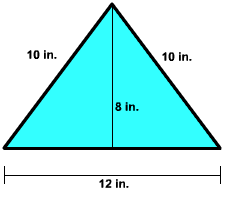
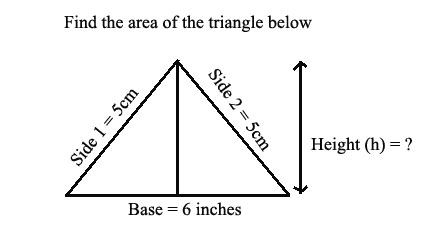
Exercise 3 Find the area of the area of the triangle shown below
Answer:
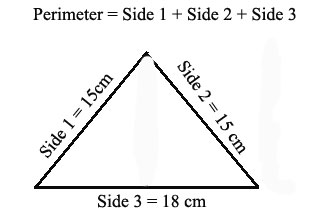
The perimeter of a polygon is equal to the distance all the way around the figure. So to calculate the perimeter of a triangle add the lengths if its sides together.
The perimeter of the above triangle is Perimeter = 18 cm + 15 cm + 15 cm = 48 cm
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
Exercise 4 Find the perimeter of the triangle from Exercise 3 (shown below)
Answer:
You may see a triangle area problem on the CAHSEE in which you do not know the height of the triangle.
These types of problems require that you know how to use the Pythagorean Theorem. This will be taught in a later lesson, but follow the link if you wish to look at that lesson now.
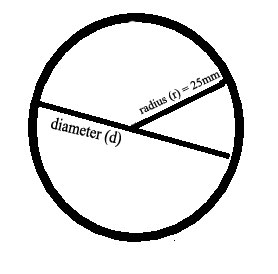
3. Finding the Area and Circumference of a Circle Definition: A circle is the set of all points in a plane that are a fixed distance from a given point in the plane. This fixed distance is called the radius of the circle. The example circle below has radius = 25 mm
This circle has a diameter of 50 mm. The diameter is the distance from any point on the circle, through its center, to a point on the opposite side of the circle. The radius of a circle is equal to half the diameter. Radius = 1/2 Diameter
To calculate the area of a circle multiply 3.14 times the radius, r, of the circle squared. Area of a Circle ≈ 3.14 r2 which is the same thing as multiplying 3.14 by the radius and then
again by the radius. Area = 3.14 x 25 mm x 25 mm = 1962.5 mm2
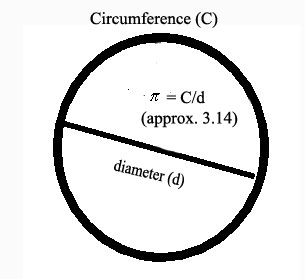
To calculate the circumference of the circle multiple
3.14 by its
diameter. Notice this is the same thing as multiplying
3.14 by two
times the radius of the circle.
The circumference of the above circle is Circumference = 3.14 x 50 mm = 157 mm
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
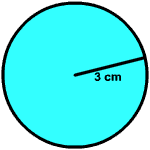
Exercise 5 Find the area and circumference of the circle shown below.
Answer:
On the CAHSEE you might be given a question involving a circle in
which you are given the diameter but not the radius. To calculate the
radius just divide the diameter in half. For instance, you know that the
diameter in the circle above is 50
mm, so the radius is half of that
number: 25 mm.
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
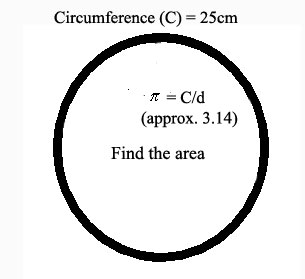
Exercise 6 Find the area of the circle that has a circumference of 50 inches. Answer:
4. Typical CAHSEE Type Question
b. Now find the perimeter of the grassy region and the flower bed so
that we know how much material needs to be purchased to fence both. Circumference of circular flowerbed
= 3.14 x d Adding these two together gives us Total = Perimeter of Grassy Region + Circumference of Circular Flowerbed = 85.7 ft.
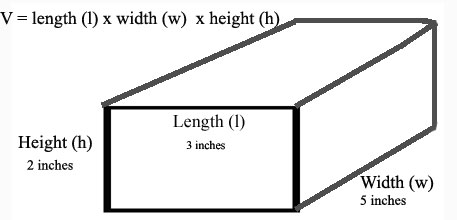
5. Finding the volume of a Rectangular Solid Definition: A rectangular solid is a 3 dimensional object in which each of its 6 faces is a rectangle and adjacent faces are perpendicular. A rectangular solid has three dimensions, length, width and height.
The rectangular solid above has length 3 inches, width 5 inches and height 2 inches. Definition: Volume is the amount of space occupied by a three-dimensional object, expressed in cubic units. To calculate the volume of a rectangular solid you multiple the area of its base times its height. So for the example above the volume is length times width (area of rectangle) times height. The volume of this rectangular solid is
Volume = (3)(5)(2) = 30
inches3
Now try one by yourself. If you want to see the answer, put your mouse
on the yellow rectangle and the answer will appear.
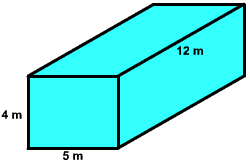
Exercise 7 Find the volume of the rectangular solid shown below.
Answer:
|