Congruent Polygons

and the Effect that

Scaling has on Area and Volume

In this lesson we will work on recognizing polygons that are congruent, matching congruent sides and angles.  We will also see how the area of a region changes when the dimensions of the sides are all changed by a constant scaling factor.  We will also look at how the volume of a solid changes when the dimensions of the solid are all changed by a constant scaling factor. 

First we look at congruent polygons.

Definition  (Congruent Polygons)

Two polygons are congruent if their corresponding sides and angles are congruent.

Note:  Two sides are congruent if they have the same length and angles are congruent if they have the same measure.

We indicate that angles are congruent by putting the same number of slash marks through each angle.  Congruent polygons necessarily have to have the same shape and the same size.  They also have to have the same number of sides.  We can think of congruent polygons as coming from the same stamp.  The location where they reside may differ and rotating or flipping congruent polygons does not change the fact that they are congruent.

Example 1

Consider the polygon shown below. 

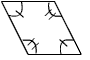
Determine which could be congruent to the above parallelogram.

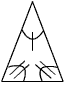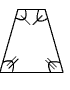A.          B.         C. 

Solution

First notice that polygon A has three sides while the given polygon has 4 sides.  These cannot be congruent.  Polygon B has the correct number of sides, but the congruent angles in polygon B are adjacent (next to each other) while the congruent angles in the given polygon are opposite angles.  In fact Polygon B is a trapezoid, while the given Polygon is a parallelogram.  Polygon B cannot be congruent to the given polygon.  Polygon C has four sides, and the opposite angles are congruent, just like the given polygon.  Polygon C could be congruent to the given polygon.  Notice that Polygon C has a vertex pointing downward while the given polygon does not.  This is irrelevant, since rotating a polygon does not change which polygons it is congruent to.

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 1

Consider the polygon shown below. 

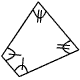
Determine which could be congruent to the above parallelogram.

A.          B.         C. 

Answer:

Once we have determined that two polygons are congruent, we can then look at corresponding sides and corresponding angles and state that their measures are equal.  You can tell  which side is equal to which by following the order that the vertices are stated. 

Example 2

Polygons ABCDEF and GHIJKL are congruent.  which sided is congruent to the side CD?

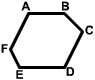
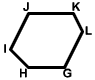
Solution

First note that other than the congruency statement, no other information is given.  You cannot just look at the figures and try to estimate the length is side CD and then try to find a side that looks as though it has the same length.  Instead, pay attention to the order at which the letters are presented.  In particular C is the third vertex named in ABCDEF and D is the fourth vertex.  We can now count from G until we get to the third and fourth named vertex in GHIJKL.  These are I and J.  We can conclude that IJ is congruent to CD.

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 2

The two polygons ABCD and EFGH are congruent.  Which side is congruent to side BC? 

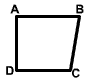
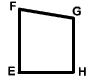
Answer:

We next ask the question, "When two regions have the same shape, but the dimensions of the second region are all the same constant multiple of the dimensions of the first region, how are their areas related?  It turns out that the area of the second object can be found by using the following formula:

        Area of second region  =  (Area of first region)(scaling factor)²

Example 3

Consider the two triangles shown below.  If the area of the first triangle is 15 square meters and each of the sides of the second triangle is exactly twice as long as the corresponding sides on the first triangle, find the area of the second triangle.

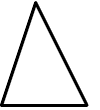
Solution

Since these triangle are the same shape but different sizes, we can use the formula above.  We have

        Area of first region  =  15

        Scaling factor  =  2

so that

        Area of second region  =  (15)(2)²

                                            =  (15)(4)

                                            =  60

So the area of the second region is 60 square meters.

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 3

A photograph is taken of a table.  The dimensions of the photograph are exactly 1/20 of the corresponding dimensions of the actual table.  The area of the photograph is measure to be 0.06 square feet, what is the area of the actual table?

Answer:

There is also a formula that relates volumes of one solid to that of another solid that is the same shape but different dimensions.  This formula is:

       Volume of second solid  =  (Volume of first solid)(scaling factor)³

Notice that the main differences between this and the formula for area are

        1.  We are finding volumes instead of areas

        2.  The second factor is cubed instead of squared

You can remember the second difference by noticing that area measurements are taken in square units such as square feet while volume measurements are taken in cubic units such as cubic feet.

Example 4

The cone shown on the left has a volume of 25 cubic centimeters.  The cone to the right of it has the same shape, but the radius and height of the right cone are 3 times as large as the radius and height of the cone on the left.  Find the volume of the cone on the right.

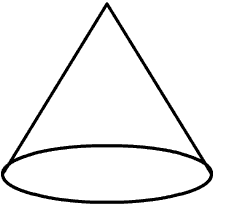
Solution

We have

       Volume of the first solid  =  25

        Scaling factor  =  3

so that

        Volume of second solid  =  (25)(3)³

                                              =  (25)(27)

                                              =  675

So the volume of the second solid is 675second cubic centimeters. 

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 4

A partially blown spherical balloon is filled with 0.5 cubic feet of air.  If the balloon is blown in such a way that the fully blown balloon is still spherical in shape, but the radius of the fully filled balloon is twice the radius of the partially blown up balloon, how many cubic feet of air will be in the fully blown balloon?

Answer: