
Absolute Value Equations and Inequalities
Absolute Value Equations
Sometimes negative numbers appear in our bank accounts, elevation measurements, and temperature; however, most of the time we only deal with positive numbers. For instance, we would probably say, "My checking account is overdrawn by fifty dollars", rather than "There is negative fifty dollars in my checking account." When we measure the distance that we have travelled or the speed that we went, it only makes sense to cite a positive number. The math symbol that tells us to drop the negative sign is the absolute value symbol. For example the absolute value of -5, written |-5| is 5. The absolute value tells us to make the result positive, it does not turn subtraction into addition. For example, do not make the mistake of thinking that
| x - 3|
is the same as
x + 3
For example if x = 5, then
|x - 3| = |5 - 3|
= | 2 |
= 2
while
x + 3 = 5 + 3
= 8
If we know what the absolute value of a number is, then we do not necessarily know what the original number is. For example if the absolute value of a number is 3, then the original number can be either 3 or -3. Symbolically if


Now that we understand how to solve absolute value equations, we will look at the process of solving absolute value inequalities. The process will be very similar to solving absolute value equations, but there will be some extra details that we will need to pay attention to. Here is an example.
Example 4
If x is an integer, what is the solution to
|x - 4| < 3
Solution
In order for |x - 4| to be less than 3, x - 4 cannot be greater than or equal to 3 and it cannot be less than or equal to -3. That is, x - 4 must be between -3 and 3. We can write this as
-3 < x - 4 < 3
We want x by itself, so we add 4 to all three sides
1 < x < 7
Since x is an integer, we take all the integers between and not including 1 and 7. Notice that we do not include 1 and 7 since the inequality is a "<" instead of a "<". The solution is
{2,3,4,5,6}
Now you try one.
Exercise 4
If x is an integer, what is the solution to
|x - 5| < 2
Solution

If the inequality is "<" or ">", then we include the endpoints. Here is an example where this occurs.
Example 5
If x is an integer, what is the solution to
|x - 2| + 1 < 5
Solution
First isolate the absolute value by subtracting 1 from both sides of the inequality.
|x - 2| < 4
In order for |x - 2| to be less or equal to 4, x - 2 must be between -4 and 4. We can write this as
-4 < x - 2 < 4
We want x by itself, so we add 2 to all three sides
-2 < x < 6
Since x is an integer, we take all the integers between and including -2 and 6. Notice that we include -2 and 6 since the inequality is a "<" instead of a "<". The solution is
{-2,-1,0,1,2,3,4,5,6}
Now it's your turn
Exercise 5
If x is an integer, what is the solution to
2|x + 3| < 2
Solution

The last two examples and exercises asked to find integer solutions to the inequality. The answers were lists of numbers. If instead we are asked to find real number solutions to the inequality, then there are an infinite number of solutions and we cannot list them all. Instead, we place the solution on a number line. If the inequality is a "<" or ">", we use parentheses"( )" for the endpoints and if the inequality is a "<" or a ">" we use square brackets "[ ]". Here is an example.
Example 6
Find all real number solutions to
|x + 1| < 4
and sketch the solution on a number line.
Solution
As with the prior two examples, we first change the absolute value inequality into a compound inequality.
-4 < x+1 < 4
Next, subtract 1 from all three sides to get
-5 < x < 3
We can now place this on a number line, using square brackets at the endpoints.
![number line with solution [-5,3]](numberLine6.jpg)
Now you try one.
Exercise 6
Which of the following displays all real number solutions to
|x + 3| < 2
A. 
B. 
C. ![number line with [-5,-1]](xerc6C.jpg)
D. ![number line with [-5,-1]](exerc6D.jpg)
Solution

Find all real number solutions to
|x + 2| > 4
and sketch the solution on a number line.
Solution
In order for x to be a solution we must have either
x + 2 < -4 Or x + 2 > 4
Subtracting 2 from both sides of each inequality gives
x < -6 Or x > 2
On the number line, the solution will be two rays, one for each inequality. It is shown below
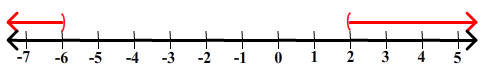
Now you try one.
Exercise 7
Which of the following displays all real number solutions to
|x + 1| > 2
A.
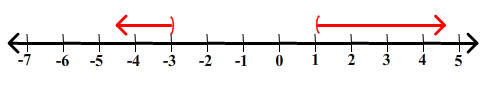
B.
![number line (-infinity,-3] [1,infinity)](exerc7B.jpg)
C. ![number line [-3,1]](exerc7C.jpg)
D. 
Solution
