MATH 204 PRACTICE EXAM I
Please work out each of the given
problems on your own paper. Credit
will be based on the steps that you show towards the final answer.
Show your work.
Problem 1
Solve the following
differential equations.
A.
(25 points)
x + y
y' =
x + 4y
This is a homogeneous differentiable equation. Let
v = y/x y = xv y' = v + xv'
x +
xv
1 + v
v + xv' = =
x +
4xv
1 + 4v
1 + v - v(1 + 4v)
xv' =
subtracting v and placing under a common denominator
1 +
4v
1 - 4v2
=
1 + 4v
1 + 4v
dv = dx/x Since
v' = dv/dx and then separate and factor.
(1 - 2v)(1 +
2v)
Now use partial fractions
1 +
4v
A
B
=
(1 - 2v)(1 +
2v)
1 -
2v
1 + 2v
A(1 + 2v) + B(1 - 2v) = 1 + 4v
v = 1/2: 2A = 3 A = 3/2
v = -1/2: 2B = -1 B = -1/2
This yeilds
3/2
-1/2
+
dv = dx/x
1 -
2v 1 + 2v
Now integrate both sides to get
-3/4 ln|1 - 2v| - 1/4 ln|1 + 2v| = ln|x| + C1
ln|(1 - 2v)3(1 + 2v)| = ln|x-4| + C2
|(1 - 2v)3(1 + 2v)| = C x -4
|(1 - 2y/x)3(1 + 2y/x)| = C x -4
|(x - 2y)3(x + 2y)| = C
B. (25 points) (ey + e -x)dx + (ey + 2ye-x)dy = 0
We find an integrating factor
My = ey Nx = -2y e -x
My - Nx
ey + 2y e -x
=
= 1
N
ey + 2y e -x
We find the integrating factor by solving
dm/dx = (1)m m = ex
Now multiply the original differential equation by the integrating factor
(ex+y + 1)dx + (ex+y + 2y)dy = 0
This transformed differential equation is exact. We can find the potential function.
fx = ex+y + 1
Integrate with respect to x to get
f(x,y) = ex+y + x + C(y)
Now take the partial derivative with respect to y to get
fy = ex+y + C'(y) = ex+y + 2y
C'(y) = 2y C(y) = y2
Finally the solution is
ex+y + x + y2 = C
C.
(25 points)
y
y' = A -
B - Ct
.
A(B - Ct)
Solution:
y =
+ k(B - Ct)1/C
1 - C
We can rewrite as
y
y' +
= A
B - Ct
This is a first order linear differential equation. We find the integrating factor
![]()
Multiplying by the integrating factor gives
(B - Ct)-1/Cy' + (B - Ct)-1/C - 1y = A(B - Ct)-1/C
((B - Ct)-1/Cy)' = A(B - Ct)-1/C
Now integrate both sides
.
-A(B - Ct)-1/C
+ 1
AC(B - Ct)-1/C + 1
(B - Ct)-1/Cy =
+ k =
+
k
C(-1/C +
1)
1 - C
Now solve for y
A(B - Ct)
y =
+ k(B - Ct)1/C
1 - C
Problem 2
Currently, Lower Angora
Lake has 300 million gallons of unpolluted water in it.
Due to a gas leak in a motor boat in Upper Angora Lake, there is an
inflow of 5000 gallons per hour that contains
2 grams per gallon of MTBE.
Since it is spring, the outflow of water from Lower Angora Lake is only
4000 gallons per hour. Assume that
the MTBE is completely mixed in the water as soon as it enters the lower lake.
A.
Set up a differential equation that describes the rate of change of MTBE
in Lower Angora Lake.
This is
Rate = Rate In - Rate Out
question. First find the Rate In.
Rate In = (5000gal/hr)(2grams/gal) = 10,000 grams/hr
Now find the Rate Out. Notice that the number of gallons in the lake is given by
Gallons = 300,000,000 + 1000t
We use this to calculate the Rate Out.
x
grams
4000 gal
Rate Out =
.
300,000,000 +
1000t
1 hr
Subtracting we get
dx
4000 x grams
= 10,000 -
dt
300,000,000 + 1000t
B.
Use the result of Problem 1 Part C to determine the amount of MTBE in
Lower Angora Lake one day after the leak began.
Solution
We have
A = 10,000 B = 300,000,000/4000 = 75,000 C = 1000/4000 = 0.25
.
10,000(75,000 -
0.25t)
y =
+ k(75,000 -
0.25t)4
1 - 0.25
We find k by noticing that y(0) = 0
0 = 750,000,000/.75 + 75,0004k = 109 + 3.164 x 1019 k
k = 3.16 x 10-11
Now plug in 1 for t to get
9999.93
Problem 3
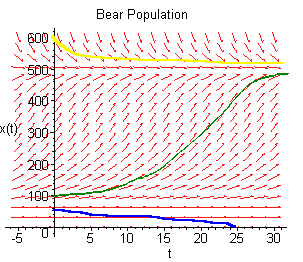
The Tahoe area has
enough resources to support up to 500 black bears, however if the bear
population declines below 50, the bears will not be able to find mates and will
eventually become extinct.
A. Set up an autonomous
differential equation that models this situation.
y' = -y(1 - y/50)(1 - y/500)
B.
Sketch the direction field for this differential equation and sketch the
solution that corresponds to the initial values:
y(0) = 45, y(0) = 100, and y(0)
= 600.
Problem 4
Solve the following differential equations.
A. y'' - 2y' + 2y = 0, y(0) = 0, y'(0) = 5
The characteristic equation is
r2 - 2r + 2 = 0
r = 1 + i or r = 1 - i
The general solution is
y = et (c1 cos t + c2 sin t)
The first initial condition gives
0 = (1)(c1) c1 = 0
So that
y = et (c2 sin t)
and
y' = c2 (et sin t + et cos t)
Now use the second initial condition
5 = c2 (0 + 1) c2 = 5
The final solution is
y = 5 et sin t
B. 3y'' - 2y' -8y = 0, y(0) = 1, y'(0) = -2Solution
3r2 - 2r - 8 = 0
This has solution
B. y'' - 4y' + 13y = 0, y(0) = 1, y'(0) = 6
Solution
First find the characteristic equation
r2 - 4r + 13 = 0
The quadratic formula or calculator gives
r = 2 + 3i or r = 2 - 3i
Thus the general solution is
y = e2t (c1cos(3t) + c2 sin(3t))
Now use the initial conditions.
Next find the derivative
y' = 2e2t (cos(3t) + c2 sin(3t)) + e2t (-3sin(3t) + 3c2 cos(3t))
Now plug in 0 to get
So that
Thus the solution is
C. y'' + 12y' + 36y = 0 y(0) = 0, y'(0) = 1
Solution
The characteristic equation is
which has repeated root solution
Thus the general solution is
The first initial condition gives
The derivative is
Plugging in 0 gives
Thus the solution to the initial value problem is
Problem 5
Please answer the
following true or false. If false,
explain why or provide a counter-example. If
true, explain why.
A.
If a differential equation is autonomous then it is separable.
True, if
dy/dx = f(y)
then
dy/f(y) = dx
separates the variable.
B. The initial value problem y' - sin(t2) + et y = 0, y(1) = 4 is guaranteed to have a unique solution defined for all values of t.
True, this is a first order
linear differential equation with continuous p(t) and
q(t). Therefore
there is a unique solution for all values of t.
C.
The difference equation yn+1
= kyn
has solution yn = y0ekn
False, the solution is
yn = y0kn
D.
d3y
dy
x
+ ln(1 - x2)
= x cos x
dx3
dx
is a third order linear
differential equation.
True, the highest derivative is y''', and the coefficients in front of y''' and y' are both functions of x.
E. The function y = t sin t
cannot
be a solution of the differential equation.
with p,and q continuous
Solution
True
First note that
y(0) = 0
and that
y' = sin t + t cos t
so that
y'(0) = 0
If
y = t sin t
is a solution and y2 is another solution such that the two solutions are linearly independent, then the Wronskian matrix at t = 0 would have its first column 0, hence the determinant would be zero. But is the Wronskian is zero for one value of t, then it is 0 for all values of t. But linearly independent solutions do not have a 0 Wronskian. Thus y = t sin t cannot be a solution.
Extra Credit: Write down one thing that your instructor can do to make the class better and one thing that you want to remain the same in the class.
(Any constructive remark will be worth full credit.)