A Sketch of the Proof of the Existence and Uniqueness Theorem

Recall the theorem that says that if a first order differential satisfies continuity conditions, then the initial value problem will have a unique solution in some neighborhood of the initial value.  More precisely,

 

Theorem (A Result For Nonlinear First Order Differential Equations)

Let

           y'  =  f(x,y)      y(x0)  =  y0 

be a differential equation such that both partial derivatives 

          fx      and      fy

are continuous in some rectangle containing (x0,y0)

Then there is a (possibly smaller) rectangle containing (x0,y0) such that there is a unique solution  f(x) that satisfies it.

 Although a rigorous proof of this theorem is outside the scope of the class, we will show how to construct a solution to the initial value problem.  First by translating the origin we can change the initial value problem to 

        y(0)  =  0

Next we can change the question as follows.  f(x) is a solution to the initial value problem if and only if 

        f'(x)  =  f(x,f(x))  and f(0)  =  0

Now integrate both sides to get

       

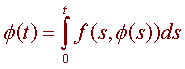
Notice that if such a function exists, then it satisfies f(0)  =  0.

The equation above is called the integral equation associated with the differential equation.

It is easier to prove that the integral equation has a unique solution, then it is to show that the original differential equation has a unique solution.  The strategy to find a solution is the following.  First guess at a solution and call the first guess f0(t).  Then plug this solution into the integral to get a new function.  If the new function is the same as the original guess, then we are done.  Otherwise call the new function f1(t).  Next plug in f1(t) into the integral to either get the same function or a new function f2(t). Continue this process to get a sequence of functions fn(t).  Finally take the limit as n approaches infinity.  This limit will be the solution to the integral equation.  In symbols, define recursively

        f0(t)  =  0

       

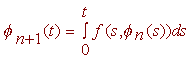
Example

Consider the differential equation

        y'  =  y + 2        y(0)  =  0

We write the corresponding integral equation

       

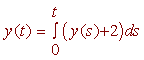
We choose 

        f0(t)  =  0

and calculate

       

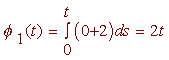
and 

       

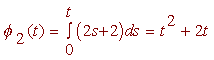
and

       

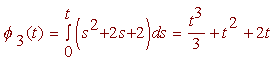
and 

       

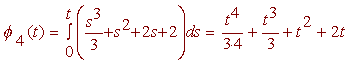
Multiplying and dividing by 2 and adding 1 gives 

      f4(t)                     t4             t3           t2           t           1
               + 1  =                   +           +           +           +            
         2                      4.3.2        3.2          2           1            1

The pattern indicates that 

      fn(t)                    tn       
               + 1  =    S         
         2                       n!      

or

      f(t)                     
               + 1  =   et 
         2                   

Solving we get

        f(t)  =  2(et - 1)

This may seem like a proof of the uniqueness and existence theorem, but we need to be sure of several details for a true proof.  

  1. Does fn(t) exist for all n.  Although we know that f(t,y) is continuous near the initial value, the integral could possible result in a value that lies outside this rectangle of continuity.  This is why we may have to get a smaller rectangle.

  2. Does the sequence fn(t) converge?  The limit may not exist.

  3. If the sequence fn(t) does converge, is the limit continuous?

  4. Is f(t) the only solution to the integral equation?  

 

Back to the First Order Differential Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions