Higher Order Differential Equations

Recall that the order of a differential equation is the highest derivative that appears in the equation.  So far we have studied first and second order differential equations.  Now we will embark on the analysis of higher order differential equations.  We will restrict our attention to linear differential equations.  The general linear differential equation can be written as

                        dⁿy                   d^n-1y                             dy    
        L(y)  =               +  p₁(t)              + ^{. . .}  + p_n-1(t)             +  p_n(t)y  =  g(t) 
                         dt                      dt                                 dt

The good news is that all the results from second order linear differential equation can be extended to higher order linear differential equations.  We list without proof the results

• If p₁, ... p_n are continuous on an interval [a,b] then there is a unique solution to the initial value problem, where instead of the initial conditions y(0)  =  y₀ and y'(0)  =  y'₀ , we need the initial conditions
  
          y(0)   =  y₀ ,   y'(0)  = y'₀,   y''(0)  =  y''₀,    ...   ,   y^(n-1)(0)  =  y^(n-1)₀ 
  
• L(y) is a linear transformation, that is 
  
          L(c₁y₁+ x₂y₂ + ... + c_ny_n)  =  c₁L(y₁) + c₂L(y₂) + ... + c_nL(y_n)
  
• If y₁, y₂ ... y_n are solutions to L(y)  =  0, then c₁y₁+ x₂y₂ + ... + c_ny_n is also a solution.
  
• For differentiable functions y₁, y₂ ... y_n, we define the Wronskian by
  
         
  
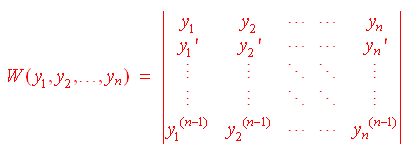
• Differentiable functions y₁, y₂ ... y_n are linearly independent if the Wronskian is nonzero for some t in [a,b].
  
• L(y)  =  0 has n linearly independent solutions.
  
• If y_h is the general solution to L(y)  =  0 and if y_p is a particular solution to L(y)  =  g(t), then y_h + y_p is the general solution to L(y)  =  g(t).
  
• Abel's theorem still holds.  That is, if y₁, y₂ ... y_n are linearly independent solutions of L(y)  =  0, then
  
         
  
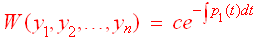
• The method of reduction of order still works.  If y₁ is a solution to L(y₁)  =  0, then L(v₁y₁) can be reduced to a differential equation of degree n - 1.

Example

Determine if the following functions are linearly independent

        y₁  =  e^2x         y₂  =  sin(3x)        y₃  =  cos x

Solution

First take derivatives

        y'₁  =  2e^2x         y'₂  =  3cos(3x)        y'₃  =  -sin x

        y''₁  =  4e^2x         y''₂  =  9sin(3x)        y''₃  =  -cos x

The Wronskian is

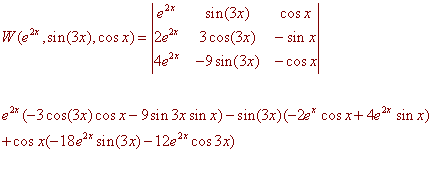
Now plug in x   =  0 (or any other value for x) to get

        (1)(-3 - 0) - (0)(-2 + 0) + (1)(0 - 12)  =  -15

In particular, since this is a nonzero number, we can conclude that the three functions are linearly independent.

Example

Use Abel's theorem to find the Wronskian of the differential equation

        ty^(iv) + 2 y''' - te^ty'' + (t³ - 4t)y' + t²sin ty  =  0

Solution

We first divide by t to get

        y^(iv) + 2/t y''' - e^ty'' + (t² - 4)y' +  t sin t y  =  0

Now take the integral of 2/t to get

        2ln t

The Wronskian is thus

       c e^{2ln t}  =  c t²

Back to the Application and Higher Order Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions