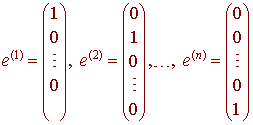Theory of Systems of Linear Differential Equations

Theory of Systems of Linear Differential Equations

It turns out that the theory of systems of linear differential equations resembles the theory of higher order differential equations. This discussion will adopt the following notation. Consider the system of differential equations

         x₁' = p₁₁(t) x₁ + ... + p_1n(t) x_n + g₁(t)
          |           |                        |                |
         x_n' = p_n₁(t) x₁ + ... + p_n_n(t) x_n + g_n(t)

We write this system as

x' = P(t)x + g(t)

A vector x = f(t) is a solution of the system of differential equation if

f' = P(t)f + g(t)

If g(t) = 0 the system of differential equations is called homogeneous. Otherwise, it is called nonhomogeneous.

Thoerem (The solution space is a vector space)

Suppose that x⁽¹⁾, x⁽²⁾, ... , x^(k) are solutions to the homogeneous system of differential equations

x' = P(t)x

Then

c₁x⁽¹⁾ + c₂x⁽²⁾ + ... + c_kx^(k)

is also a solution for any constants c₁, c₂, ... , c_k

Just as we had the Wronskian for higher order linear differential equations, we can define a similar beast for systems of linear differential equations.

x⁽¹⁾, x⁽²⁾, ..., x⁽ⁿ⁾

are n solutions of an n x n system, then the Wronskian of this set is the determinant of the matrix whose i^th column is x⁽ⁱ⁾.

Example

Let

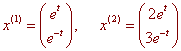
Then

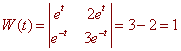
It is a direct consequence from linear algebra that solutions are linearly independent if and only if the Wronskian is nonzero. In fact, more is true. There is a generalizations of Abel's theorem for systems of linear differential equations.

         dW
                    = (p₁₁ + p₂₂ + ... p_nn)W        (Abel's Theorem)
           dt

The main theorem on uniqueness and existence of solutions of systems of differential equations also holds true. We state it below.

Theorem (Existence and Uniqueness for Systems)

Let

x' = P(t)x

be a differential equation with p_ij continuous for all i and j on the interval a < t < b. Then there exists n unique linearly independent solutions. If the initial value

x(0) = x₀

is given, then there exists a unique solution in the interval (a,b).

In particular, if

x⁽¹⁾, x⁽²⁾, ..., x⁽ⁿ⁾

are solutions of the homogeneous system, and if the Wronskian is nonzero, then

y = c₁x⁽¹⁾ + c₂x⁽²⁾ + ... + c_kx^(k)

is the general solution to the system. We call x⁽¹⁾, x⁽²⁾, ..., x⁽ⁿ⁾ a fundamental set of solutions to the system of differential equations.

In particular, if the Wronskian matrix at t₀ is the identity matrix (W(t₀) = I) then its determinant is one hence not zero. This gives us the following theorem

Theorem

Let

If x⁽¹⁾, x⁽²⁾, ... , x⁽ⁿ⁾ are solutions to the homogeneous system of differential equations satisfying the conditions

x⁽¹⁾(t₀) = e⁽¹⁾, x⁽²⁾(t₀) = e⁽²⁾, ... , x⁽ⁿ⁾(t₀) = e⁽ⁿ⁾

then they form a fundamental set of solutions.

Back to the Power Series Methods and Laplace Transforms Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions