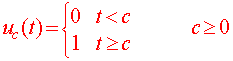Step Functions
In this discussion, we will investigate piecewise defined functions and their Laplace Transforms. We start with the fundamental piecewise defined function, the Heaviside function.
| Definition: The Heaviside function
The Heaviside function, also called the unit step function, is defined by
|
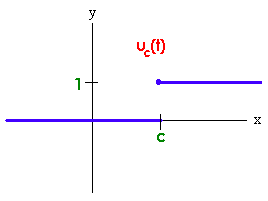
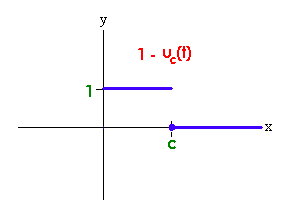
The Heaviside function y = uc(t) and y = 1 - uc(t) are graphed below.
Example
We can write the function
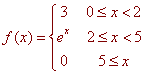
In terms of Heaviside functions.
Solution
We tackle the functions in parts. The function that is 1 from 0 to 2 and 0 otherwise is
1 - u2(x)
Multiplying by 3 gives
3(1 - u2(x)) = 3 - 3u2(x)
To get the function that is 1 between 2 and 5 and 0 otherwise, we subtract
u2(x) - u5(x)
Now multiply by ex to get
ex(u2(x) - u5(x)) = ex u2(x) - ex u5(x)
Adding these together gives
f(x) = 3 - 3u2(x) + ex u2(x) - ex u5(x)
= 3 + (ex - 3)u2(x) - ex u5(x)
We can find the Laplace transform of uc(t) by integrating
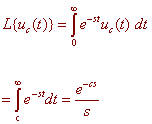
|
e-cs L{uc(t)} = s |
In practice, we want to find the Laplace transform of a more general piecewise defined function such as
![]()
This type of function occurs in electronics when a switch is suddenly turned on after one second and a forcing function is applied. We can write
f(x) = up(x) sin x
We will be interested in the Laplace transform of a product of the Heaviside function with a continuous function. The result that we need is
|
L{uc(t) f(t - c)} = e-cs L{f(t)} |
By taking inverses we get that if F(s) = L{f(t)}, then
L-1{e-csF(s)} = uc(t)f(t - c)
Proof
We use the definition to get
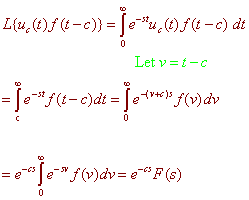
Example
Find the Laplace transform of
![]()
Solution
We use that fact that
f(x) = up(x)sin x = -up(x) sin[(x - p)]
Now we can use the formula to get that
L{f(x)} = -L{up(x) sin[(x - p)]} = -e-cs L{sin x}
By the table, we get
-e-cs
=
s2 + 1
Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions