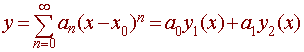Series Solutions and Convergence
In the last section, we saw how to find series solutions to second order linear differential equations. We did not investigate the convergence of these series. In this discussion, we will derive an alternate method to find series solutions. We will also learn how to determine the radius of convergence of the solutions just by taking a quick glance of the differential equation.
Example
Consider the differential equation
y'' + y' + ty = 0
As before we seek a series solution
y = a0 + a1t + a2t2 + a3t3 + a4t4 + ...
The theory for Taylor Series states that
n!an = y(n)(0)
We have
y'' = -y' - ty
Plugging in 0 gives
2!a2 = y''(0) = -y'(0) + 0 = -a1
a2 = -a1/2
Taking the derivative of the differential equation gives
(y'' + y' + ty)' = y''' + y'' + ty' + y = 0
or
y''' = -y'' - ty' - y
Plugging in zero gives
3!a3 = a1 - a0
a3 = a1/6 - a0/6
Taking another derivative gives
(y''' + y'' + ty' + y)' = y(iv) + y''' + ty'' + 2y' = 0
or
y(iv) = -y''' - ty'' - 2y'
Plugging in zero gives
4!a4 = -a1 + a0 - 2a1
a4 = -49/24 a1 + a0/24
The important thing to note here is that all of the coefficients can be written in terms of the first two.
To come up with a theorem regarding this, we first need a definition.
|
Definition A function f(x) is called analytic at x0 if f(x) is equal to its power series. |
It turns out that if p(x) and q(x) are analytic then there always exists a power series solution to the corresponding differential equation. We state this fact below without proof. If x0 is a point such that p(x) and p(x) are analytic, then x0 is called an ordinary point of the differential equation.
|
Theorem Let x0 be an ordinary point of the differential equation L(y) = y'' + p(t)y' + q(t)y = 0 Then the general solution can be represented by the power series
where a0 and a1 are arbitrary constants and y1 and y2 are analytic at x0. The radii of convergence for y1 and y2 are at least as large as the minimum radii of convergences for p and q. |
Remark: The easiest way of find the radii of convergence of most functions us by using the following fact
If f(x) is an analytic function for all x, then the radius of convergence for 1/f(x) is the distance from the center of convergence to the closest root (possibly complex) of f(x).
Example
Find a lower bound for the radius of convergence of series solutions about x = 1 for the differential equation
(x2 + 4)y'' + sin(x)y' + exy = 0
Solution
We have
sin
x
ex
p(x)
=
q(x) =
x2 +
4
x2 + 4
Both of these are quotient of analytic functions. the roots of x2 + 4 are
2i and -2i
The distance from 1 to 2i is the same as the distance from (1,0) to (0,2) which is
![]()
We get the same distance from 1 to -2i.
Hence the radii of convergence of the solutions are both at least ![]() .
.
Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions