Regular Singular Points
When we worked out series solutions to differential equations in previous discussions, we always assumed that x0 was an ordinary point, that is p and q converged to their Taylor Series expansions. What happens if the point is a singular point?
Example
Attempt to find the solution to
xy'' + y = 0 y(0) = 1, y'(0) = 2
Solution
As before, we let
![]()
Take derivatives
![]()
Now we plug these into the original differential equation
![]()
Let
u = n - 1 n = u + 1
And change back to n to get
![]()
Plugging in 0 into the second summand and combining, we get
![]()
Now comes the twist. From the initial conditions, we get
a0 = 1 and a1 = 2
However, equating coefficients, we get
a0 = 0
-an
an+1
=
n(n + 1)
We get a contradiction, since a0 cannot be both 0 and 1. We can conclude that there is no McLaurin series solution to the differential equation. This does not mean that there is no solution at all, just not a series solution.
What is going on here is that 0 is a singular point for this differential equation. When we have a singular point, all bets are off as to what type of solution we can have. Some have no analytic solutions, others have one analytic solution and one non-analytic solution, and still others have two analytic solutions. There is a classification of singular points that are particularly tame. We describe this class below.
|
Definition of Regular Singular Points Let P(x)y'' + Q(x)y' + R(x)y = 0 be a linear second order differential equation. Then x0 is called a regular singular point if
and
are both finite. |
A singular point that is not a regular singular point is called an irregular singular point. Another way of defining singular points is to say that
(x - x0)p(x) and (x - x0)2
both have a removable discontinuity at x0.
Example
Find all regular and irregular singular points for the differential equation
(x sin x)y'' + (cos x)y' + ex y = 0
Solution
The zeros of x sin x are
x = kp for k an integer.
These are the singular points for the equation. Now we test for regularity. First test at x = 0.
![]()
This limit is undefined hence the singularity at x = 0 is irregular. Note that once one of the two limits is not finite, the point is automatically irregular regardless of the other limit.
Now we test the rest of the points
![]()
The first factor has a finite limit. For the second factor, we can use L'Hopital's rule to get
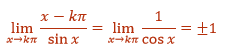
We are half way to being regular. Now find
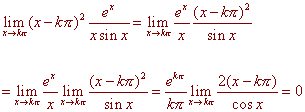
Since both limits are finite, x = kp for k nonzero are regular singular points.
We may ask what all the fuss is about? For differential equations, just about all the points will be nonsingular. Why can't we just ignore the few points that are singular. The answer is that the singular point is where the interesting part occurs. Ignoring the singular point would be like deciding to ignore black holes in the study astronomy because most of space is not a black hole.
Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions