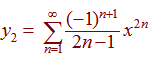Solve
![]()
Solution
Let
![]()
then
![]() and
and
![]()
We can write the differential equation as
![]()
Substituting back into this differential equation and multiplying the x2 through gives
![]()
We next need to make the second term has the nth power of x instead of n-2. For this term, we let
u
= n – 2,
n =
u + 2
The second term becomes
![]()
now changing this back to n and placing the term back into the differential equation gives
![]()
Since they sums do not all start at the same number, we pull out the n = 0 and n = 1 terms to get
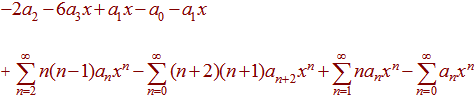
or
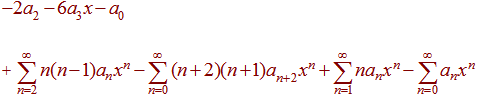
We can now combine the series to get
-2a2 - 6a3x - a0
![]()
We are looking for two linearly independent solutions, so we let the first one be such that
y(0)
= 0
y’(0) =
1
this implies that
a0
= 0
and
a1
= 1
from our last equation we have
0 = -2a2 – a0 = -2a2
or
a2 = 0
We also have
0 = - 6a3
or
a3 = 0
The terms from the series must all be zero, since that is what it means for a polynomial to be zero. Hence
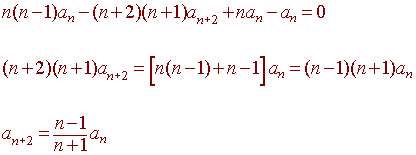
Notice that since
a2 = a3 = 0
All of the rest of the coefficients must be zero, since they are each a multiple of the coefficient two before them. Therefore the first linear independent solution is
y1 = x
For the second linearly independent solution, we let
y(0)
= 1
y’(0) =
0
this implies that
a0
= 1
and
a1
= 0
from our last equation we have
1 = -2a2 – a0 = -2a2 - 1
or
a2 = -1
We also have
0
=
-6a3
or
a3
= 0
we still have
![]()
so notice that the odd terms are all zero. For the even terms, we have
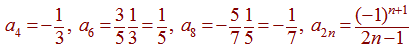
This one has the series representation