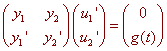
Variation of Parameters

In the last section we solved nonhomogeneous differential equations using the method of undetermined coefficients.  This method fails to find a solution when the functions g(t) does not generate a UC-Set.  For example if g(t) is sec(t), t ^-1, ln t, etc, we must use another approach.  The approach that we will use is similar to reduction of order.  Our method will be called variation of parameters.

Consider the differential equation

        L(y)  =  y'' + p(t)y' + q(t)y  =  g(t)

And let y₁ and y₂ be solutions to the corresponding homogeneous differential equation 

        L(y)  =  0

We write the particular solution is of the form 

        y_p = u₁y₁ + u₂y₂

where u₁ and u₂ are both functions of t.  Notice that this is always possible, by setting 

        u₁  =  1/y₁        and        u₂  =  (y_p - 1)/y₂ 

Actually more can be said, since we are choosing two parameters to find one solution, we can impose one additional condition on the u₁ and u₂ and still end up with a solution.  We make the assumption that 

        u₁' y₁ + u₂' y₂  =  0

This assumption will come in handy later.

Next take the derivative

        y_p' = u₁'y₁ + u₁y₁' + u₂'y₂ + u₂y₂' 

The assumption helps us simplify y_p' as 

        y_p' =  u₁y₁' +  u₂y₂' 

Now take a second derivative

        y_p'' = u₁'y₁' + u₁y₁'' + u₂'y₂' + u₂y₂''

Now substitute into the original differential equation to get

        (u₁'y₁' + u₁y₁'' + u₂'y₂' + u₂y₂'') + p(t)(u₁y₁' +  u₂y₂' ) + q(t)(u₁y₁ + u₂y₂)  =  g(t)

Combine terms with common u's, we get

        u₁(y₁'' + p(t)y₁' + q(t)y₁) + u₂(y₂'' + p(t)y₂' + q(t)y₂) + u₁'y₁' + u₂'y₂'  =  g(t)

Now notice that since y₁ and y₂ are solutions to the differential equation, both expressions in the parentheses are zero.  We have 

        u₁'y₁' + u₂'y₂'  =  g(t)

This equation along with the assumption give a system of two equations and two unknowns

        u₁' y₁ + u₂' y₂  =  0

        u₁'y₁' + u₂'y₂'  =  g(t)

Using matrices we get

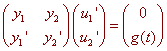
We recognize the first matrix as the matrix for the Wronskian.  Calling this W, and recalling that the Wronskian of two linearly independent solutions is never zero we can take W^-1 of both sides to get

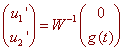
Integrate to find u₁ and u₂.  

Example

Given that 

        y₁  =  x²  and   y₂  =  x² ln x

are solutions to 

        x²y'' - 3xy' + 4y  =  x²ln x

to the corresponding homogeneous differential equation, find the general solution to the nonhomogeneous differential equation.

Solution

First, we divide by x² to get the differential equation in standard form

        y'' - 3/x y' + 4/x² y  =  ln x

We let

        y_p = u₁y₁ + u₂y₂ 

The Wronskian matrix is 

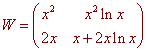
We use the adjoint formula to find the inverse matrix.  First the Wronskian is the determinant which is 

        W  =  x³ + 2x³ ln x - 2x³ ln x  =  x³ 

So the inverse is 

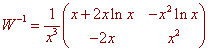
We have 

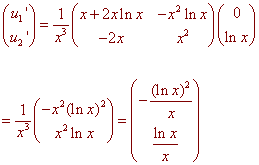
 Integrating using u-substitution gives

                    -(ln x)³
        u₁  =                  
                        3         

                    (ln x)²
        u₂  =                  
                        2         

We have 

                     
        y_p  =  -1/3 x²(ln x)³ + 1/2 x² (ln x)³  =  1/6 x²(ln x)³
                               

Finally we get

                                                
        y  =  c₁ x² + c₂ x² ln x + 1/6 x² (ln x)³

Back to the Linear Second Order Differential Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions