Inner Product Spaces
Definitions and Examples
We have seen how to take the dot product of any two vectors in Rn. In this discussion, we will generalize this idea to general vector spaces. The dot product had certain properties that we will use to define this generalized product.
Let V be a vector space and u, v, and w be vectors in V and c be a constant. Then an inner product ( , ) on V is a function with domain consisting of pairs of vectors and range real numbers satisfying the following properties.
1. (u, u) > 0 with equality if and only if u = 0.
2. (u, v) = (v, u)
3. (u + v, w) = (u, w) + (v, w)
4. (cu, v) = (u, cv) = c(u, v)
A vector space with its inner product is called an inner product space.
Notice that the regular dot product satisfies these four properties.
Example
Let V be the vector space consisting of all continuous functions with the standard + and *. Then define an inner product by
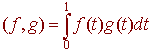
For example
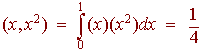
The four properties follow immediately from the analogous property of the definite integral. For example
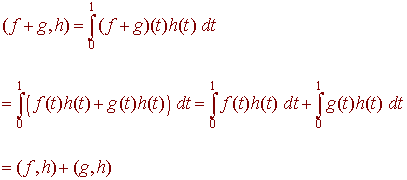
Example
Let V = R2 and consider the function
((a,b), (c,d)) = ac + 2bd
Then this function defines an inner product. We will prove Property 1. We have
((a,b), (a,b)) = a2 + 2b2 > 0
And equality occurs if and only if both a and b are 0.
Fourier Series
We will spend the rest of the discussion with a special case of an inner product space. For any inner product space V we call vectors v and w orthogonal if
(v, w) = 0
And we define the length of v by
![]()
We will call a basis S for a vector space V orthonormal if every element of S is a unit vector (length one) and any two distinct elements are orthogonal.
The inner product space that we are interested in is the space of continuous functions with
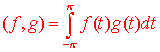
Let S = {v1, v2, v3, ...} be the infinite set of vectors (functions) defined by
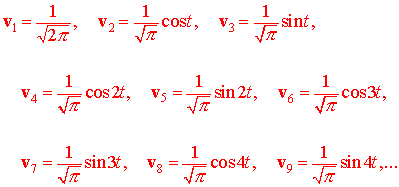
We leave it as an exercise to show that
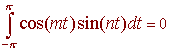
and for m and n distinct positive integers,
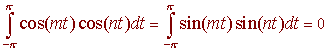
and
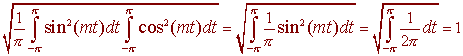
The above identities imply that S is an orthonormal set of vectors. To show that it is a basis is beyond the level of this discussion. In fact, we have yet to understand about infinite dimensional bases.
Recall that
projWv = (v,w1) w1 + (v,w2) w2 + (v,w3) w3 + ...
Notice that we have adjusted the definition to use the inner product instead of the dot product and for an infinite orthonormal set instead of a finite set. This definition provides us with a way of approximating a continuous function with elements of the orthonormal set. Ths idea is analogous to idea of the Taylor Series. When the basis is as above, the inner products are called the Fourier coefficients of the function.
Example
Calculate the first four nonzero Fourier coefficients for the function
f(t) = |t|
Solution
We have

It turns out that the next two nonzero Fourier coefficients are
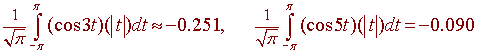
We can write
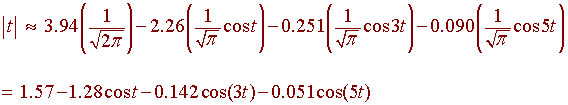
The graphs of y = |t| and the above equation are shown below.
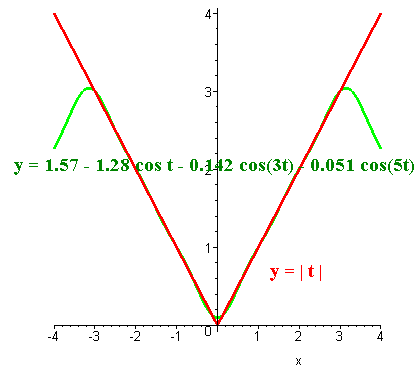
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions