Fractals

The study of fractals has recently become a hot topic.  Fractals can model real world phenomena such as coastlines, trees, and crystals.  In this discussion, we will focus on some of the most basic ideas of two dimensional fractals.

Affine Transformations

So far our transformations have all been linear transformations.  We now define a special transformation that is not a linear transformation.

Definition

Let b be a fixed vector in R². Then the function T from R² to R² defined by

        T(v)  =  v + b 

is called a translation by b.  We write

        tran_b(v)  =  v + b 

If A is a 2x2 matrix then the function defined by

        T(v)  =  Av + b 

is called an affine transformation.

We can see that an affine transformation is a composition of a linear transformation and a translation.  Note that if

        S(v)  =  Av + b        and        T(v)  =  Bv + c 

then

        S(T(v))  =  S(Bv + c)  =  A( Bv + c) + b  =  ABv + (Ac + b)

is also an affine transformation.

Recall that the vector equation for a line that is parallel to the vector u and passes through the point represented by the vector w is 

        x  =  w + tu 

If 

        T(v)  =  Av + b 

is an affine transformation, then the image of the line is 

        T(w + tu)  

which is another line.  Therefore the image of a line segment is a line segment.

Example

Consider the letter V in the xy-plane as shown in the diagram below.

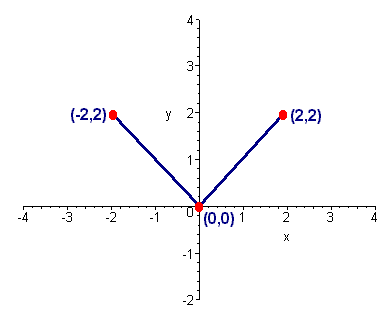
We will look at the effect of the affine transformation

        T(v)  =  Av + b 

where 

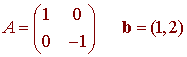
Consider the matrix 

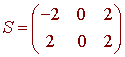
which is just the matrix whose columns are the vertices of the figure.  We have that 

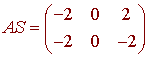
and

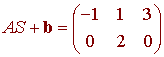
We have used the convention that adding b to matrix is done by adding b to all of the columns.  This picture is shown below.

We see that the transformation is a composition of reflection about the x-axis and translation by (1,2).

Fractals

You may be asking what affine transformations have to do with fractals.  We will consider successions of several affine transformation and see that the total image under these produce fractal images.

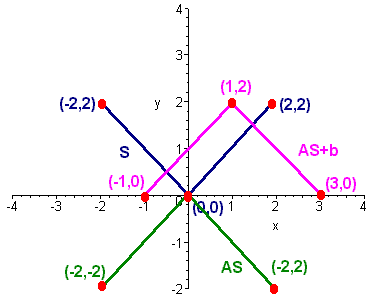
Consider the line segment of length 1.  Take out the middle third and replace it with a square (without bottom) of side length 1/3.  Then replace the middle third of each horizontal segment with a square (without bottom of side length 1/9).  We can continue this process indefinitely to get a fractal.

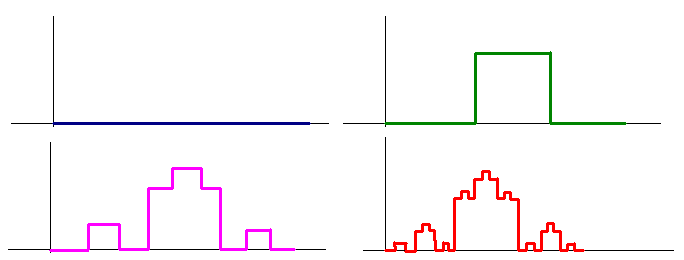
The big challenge is to figure out the transformations that create this fractal.  We notice that once a vertical line segment is created, it remains in the picture.  Hence we need to determine how the horizontal segments are transformed.  We see that each horizontal segment is converted into five separate segments.  We will need five different affine transformations for each.  Consider the first set (from the blue graph to the green graph.  We will need to first contract the segment by a factor of three.  The matrix that does this is 

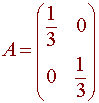
For the horizontal line segments we translate by

        b₁  =  (0,0)        b₂  =  (1/3, 1/3)    b₃  =  (2/3, 0)

For the vertical lines we need to rotate the segment by an angle of p/2.  The matrix that does this is

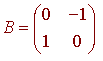
then the vertical line segments are translated by the vectors

        c₁  =  (1/3, 0)    c₂  =  (2/3, 0)

We can summarize this by saying that there are five affiine transformations given by

        T₁(x)  =  Ax    T₂(x)  =  Ax + b₁     T₃(x)  =  Ax + b₃ 

        T₄(x)  =  BAx + c₁      T₅(x)  =  BAx + c₂ 

For the next stage, we again can find the transformations needed.  Notice that each of the transformations will be compositions of  a translation followed by multiplication by A or AB and a final translation.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions