Recursive Sequences and Fibonacci Sequences

In this discussion we will see how matrices can be used to describe recursive sequences, in particular Fibonacci numbers.  Recall that a recursively defined sequence is a sequence where the first one or more values are given along with a formula that relates the n^th term to the previous terms.  The Fibonacci sequence is defined as follows:

        u_n  =  u_{n - 1} + u_{n - 2}       u₀  =  1        u₁  =  1

We can find the Fibonacci numbers by using the formula

        u₂  =  u₁ + u₀  =  1 + 1  =  2

        u₃  =  u₂ + u₁  =  2 + 1  =  3

        u₄  =  u₃ + u₂  =  3 + 2  =  5

        u₅  =  u₄ + u₃  =  5 + 3  =  8

These numbers occur in several disciplines and wherever you don't expect them in mathematics.  For example suppose one mating pair of rabbits is introduced into an ecosystem.  This breed of rabbits produce a pair of rabbits after their second month of life and all months after that.  Assume no rabbits die.  Then the zero^th  and first month, there is one pair of rabbits.  On the second month there will be two pairs:  the original pair plus their children.  The third month there will three pairs:  the two pairs from second month plus the children from the original pair.  If we want to find out how many rabbits on the n^th month, we add the number of rabbits from the prior month and the number of children.  Since only two month old rabbits can have children, we only add the rabbits that were there two months ago.  This is the Fibonacci sequence.

We can see how each number is produced, however if we want to find the 1000^th Fibonacci number this way, it would be exhausting.  We now show how matrices can be used to produce Fibonacci numbers more efficiently.  We can write the following two equations:

        u_n      =  u_{n - 1} + u_{n - 2} 
        u_{n - 1}  =  u_{n - 1} 

This has matrix equation

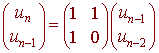
We can write this as

        w_k  =  Aw_{k - 1} 

where

Notice that 

        w₁  =  Aw₀ 
        w₂  =  Aw₁  =  AAw₀  =  A² w₀

In general, we have 

        w_k  =  A^k w₀

We now seek a fancy way to find a power of a matrix.  The answer comes with diagonalization.  We have that if A is diaogonalizable with

        A  =  PDP^-1 

then 

        A^k  =  PD^kP^-1

We can diagonalize this matrix with 

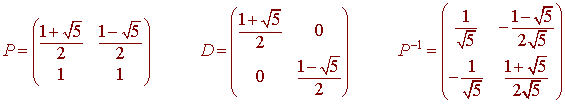
The n^th Fibonacci number can be found by 

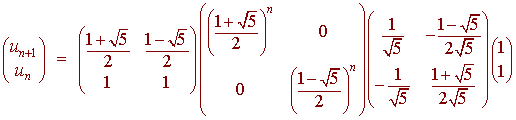
If you carefully multiply this out and take the first component of the result, we get

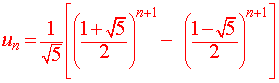
Hence the 1000^th Fibonacci number is 

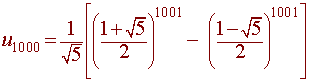
This number is extremely large.

Other Sequences

We can play this same game with modified rules.  For example, if the mature rabbits had six pairs of children instead of one, then the recursion relationship would be

        u_n  =  u_{n - 1} + 6u_{n - 2}       u₀  =  1        u₁  =  1

and the matrix equation would be

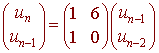
and we would use a similar technique to find a general formula for u_n.  In this case, we have

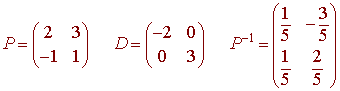
So that

Hence 

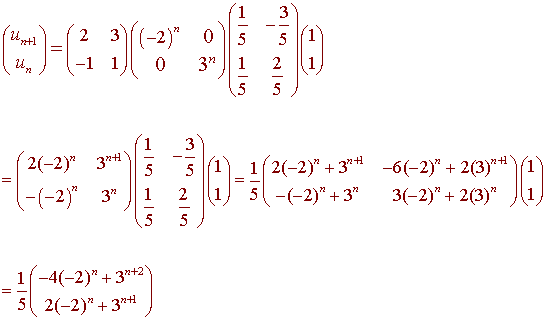
Back to the Vectors Home Page

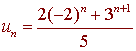
Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions