Inverse of a Matrix

Definition and Examples

Recall that functions f and g are inverses if

        f(g(x))  =  g(f(x))  =  x

We will see later that matrices can be considered as functions from Rⁿ to R^m and that matrix multiplication is composition of these functions.  With this knowledge, we have the following:

Let A and B be n x n matrices then A and B are inverses of each other, then

       AB  =  BA  =  I_n

Example

Consider the matrices

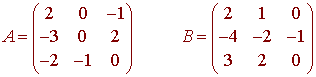
We can check that when we multiply A and B in either order we get the identity matrix.  (Check this.)

Not all square matrices have inverses.  If a matrix has an inverse, we call it nonsingular or invertible.  Otherwise it is called singular.  We will see in the next section how to determine if a matrix is singular or nonsingular.

Properties of Inverses

Below are four properties of inverses. 

1. If A is nonsingular, then so is A^-1 and
   
             (A^-1) ^-1  =  A
   
   
2. If A and B are nonsingular matrices, then AB is nonsingular and
   
           (AB) ^-1  =  B^-1A^{-1
   -1}
   
   
3. If A is nonsingular then
   
             (A^T) ^-1  =  (A ^-1)^T
   
   
4. If A and B are matrices with
   
           AB  =  I_n
   
   then A and B are inverses of each other.

Notice that the fourth property implies that if AB  =  I then BA  =  I.

The first three properties' proof are elementary, while the fourth is too advanced for this discussion.  We will prove the second.

Proof that (AB) ^-1  =  B ^-1 A ^-1

By property 4, we only need to show that

        (AB)(B ^-1 A ^-1)  =  I

We have

        (AB)(B ^-1 A ^-1)  =  A(BB ^-1)A ^-1     associative property

       =  AIA^-1        definition of inverse

        =  AA^-1       definition of the identity matrix

       =  I               definition of inverse

Finding the Inverse

Now that we understand what an inverse is, we would like to find a way to calculate and inverse of a nonsingular matrix.  We use the definitions of the inverse and matrix multiplication.  Let A be a nonsingular matrix and B be its inverse.  Then

        AB  =  I

Recall that we find the j^th column of the product by multiplying A by the j^th column of B.  Now for some notation.  Let e_j be the m x 1 matrix that is the j^th column of the identity matrix and x_j be the j^th column of B.  Then 

        Ax_j  =  e_j 

We can write this in augmented form

        [A|e_j]

Instead of solving these augmented problems one at a time using row operations, we can solve them simultaneously.  We solve

        [A | I]

Example

Find the inverse of the matrix

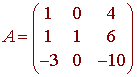
Solution

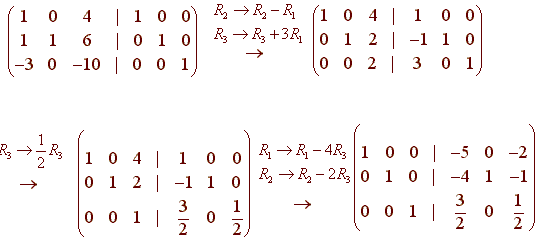
The inverse matrix is just the right hand side of the final augmented matrix

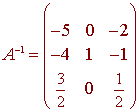
This example demonstrates that if A is row equivalent to the identity matrix then A is nonsingular.

Linear Systems and Inverses

We can use the inverse of a matrix to solve linear systems.  Suppose that

        Ax  =  b

Then just as we divide by a coefficient to isolate x, we can apply A^-1 to both sides to isolate the x. 

        A^-1Ax  =  A^-1b

        Ix  =  A^-1b        x  =  A^-1b

Example

Solve

        x + 4z  =  2
        x + y + 6z  =  3
        -3x - 10z  =  4

Solution

We put this system in matrix form

       Ax  =  b

with

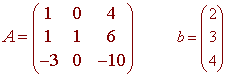
The solution is

        x  =  A^-1 b

We have already computed the inverse.  We arrive at

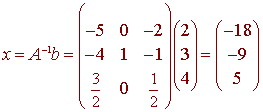
The solution is

        x  =  -18        y  =  -9        z  =  5

Notice that if b is the zero vector, then

        Ax  =  0

can be solved by

        x  =  A^-10  =  0

This demonstrates a theorem

Theorem of Nonsingular Equivalences

The Following Are Equivalent (TFAE)

1. A is nonsingular
   
   
2. Ax  =  0 has only the trivial solution
   
   
3. A is row equivalent to I
   
   
4. The linear system Ax  =  b has a unique solution for every n x 1 matrix b

Back to the Matrices and Applications Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions