Math 203 Practice Midterm 2

 

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.

 

Problem 1 

Let  L:  R2 --> R3   be a linear transformation such that 

        L (1,4) = (1,-1,3)   and     L (0,2) =  (2,1,4)

Find L(1,0)

 Solution

We need to find constants c1 and c2 such that 

        c1(1,4) + c2(0,2)  =  (1,0)

This gives 

        c1             =  1
        4c1 + 2c2  =  0 

we rref the matrix 

             

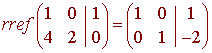
hence

        (1,0)  =  1(1,4) - 2(0,2)

Now take the linear transformation 

        L(1,0)  =  L( (1,4) - 2(0,2) )  =   L((1,4)) - 2 L((0,2))

        (1,-1,3) - 2(2,1,4)  =  (-3, -3, -5)

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 2

Of the following two subsets of the vector space of differentiable functions, determine which is a subspace.  For the one that is not a subspace, demonstrate why it is not.  For the one that is a subspace, prove that it is a subspace.

A.  S  =  {f | f(3)  =  f '(3)} 

B.  T  =  {f | f(0)f '(0)  =  0} 

 Solution

A.  This is a subspace.  We need to show that the two closure properties hold.  

If f and g are functions with 

        f(3)  =  f '(3)        and        g(3)  =  g'(3) 

then

        (f + g)(3)  =  f(3) + g(3)  =  f '(3) + g'(3)  =  (f + g)'(3)

hence f + g is in the subset.  If c is a constant, then

        (cf)(3)  =  cf(3)  =  cf '(3)  =  (cf)'(3)

hence cf is in the subset.  Since both closure properties are true, we can conclude that S is a subspace.

B.  This set is not a subspace.  Let f(t)  =  1 and g(t)  =  t.  Then 

        f(0)f '(0)  =  (1)(0)  =  0        and        g(0)g'(0)  =  (0)(1)  =  0

so both f and g are in T.  However

        (f + g)(0)(f + g)'(0)  =  [f(0) + g(0)] [f '(0) + g'(0)]  =  (1 + 0)(0 + 1)  =  1

Hence T is not closed under addition.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 3

Let  S  =  {t2, t2 + 2t, t2 + 3}  and T  =  {2t - 1, 5t - 3, t2} be subsets of P2 

A.   Prove that S is a basis for P2.

Solution

Since the dimension of P2 is 3 and S has 3 vectors, we need only prove that the vectors in S are linearly independent.  If we let 

        c1t2 + c2(t2 + 2t) + c3(t2 + 3)  =  0

then we can combine like terms to obtain

        (c1 + c2 + c3)t2 + 2c2t + 3c3  =  0

If a polynomial equals zero then each of the coefficients equal zero.  We get

        c1 + c2 + c3  =  0
                2c2       =  0
                     3c3  =  0

The matrix for this equation is

       

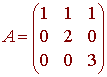
has determinant equal to 6.  Since the determinant is nonzero, the system has only the trivial solution, hence the three vectors are linearly independent.  We can conclude that S is a basis for P2.  

        

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B.  Find the transition matrix PS<--T .

Solution

Let E be a standard basis E  =  {t2, t, 1} and look at the following diagram

       

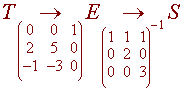
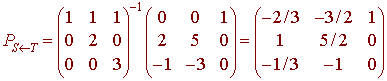
To go from T to S, we just multiply the matrices

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 4  

Prove that if A is an m x n matrix such that the columns of A are linearly independent and the rows of A are linearly independent, then m = n.

Solution

Proof:  Since the rows of A are linearly independent and there are m rows, the dimension of the row space is m.  Since the columns of A are linearly independent and there are n columns, the dimension of the column space is n.  Since the row and column space are equal (to the rank), we can conclude that m = n.

 

 

 

 

 

 

 

 

 

 

 

 

Problem 5 

Let

       

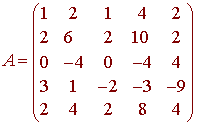
A.     Find the rank and the nullity of A. 

Solution

We find 

       

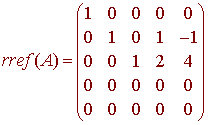
Since there are three corners, the rank of A is 3.  From the equation

        rank(A) + nullity(A)  =  n

we get

        nullity(A)  =  5 - 2  =  3

B.     Find a basis for the Null Space of A.

We use the above rref matrix to get the basis 

        {(0,-1,-2,1,0), (0,1,-4,0,1)}

C.     Find a basis for the Column Space of A using columns of A.

We can just take the columns from the corresponding corner entries.  Since the corner entries appear in the first, second, and third columns, we take these columns.

        {(1,2,0,3,2), (2,6,-4,1,4), (1,2,0,-2,2)}

D.     Find a basis for the Row Space of A using rows of A.

We find the basis for the column space of AT.  We have 

       

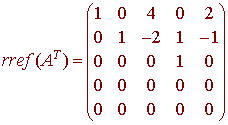
Hence we take the first, second, and fourth rows of A. 

        {(1,2,1,4,2), (2,6,2,10,2), (3,1,-2,-1,-9)}

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 6

Let  S  =  {v1, v2, ..., vn} be a set of linearly independent vectors and let v be a vector in the span of S.  Prove that v can uniquely be written as a linear combination of elements of S.  That is that prove that if

      v  =  a1v1 +a2v2 + ... + anvn        and        v  =  b1v1 +b2v2 + ... + bnvn     

then

        a1  =  b2, a2  =  b2, ... , an  =  bn 

Solution

Suppose that 

      v  =  a1v1 +a2v2 + ... + anvn        and        v  =  b1v1 +b2v2 + ... + bnvn     

Then

      a1v1 +a2v2 + ... + a2vn   =  b1v1 +b2v2 + ... + bnvn      

Moving everything to the left hand side and combining like terms, we get

        (a1 - b1)v1 + (a2 - b2)v2 + ... + (an- bn)vn   =  0

Since the vectors are linearly independent, all of the coefficients are zero, that is

        (a1 - b1)  =  (a2 - b2)  =  ...  =  (an- bn)  =  0

so that 

        a1 = b1 ,   a2  =  b2  ,  ... ,   an = bn