Math 203 Practice Midterm 2

Please work out each of the given problems.  Credit will be based on the steps towards the final answer.  Show your work.

  Printable Key

Problem 1 

Let  L:  R² --> R³   be a linear transformation such that 

        L (1,4) = (1,-1,3)   and     L (0,2) =  (2,1,4)

Find L(1,0)

  Solution

Problem 2

Of the following two subsets of the vector space of differentiable functions, determine which is a subspace.  For the one that is not a subspace, demonstrate why it is not.  For the one that is a subspace, prove that it is a subspace.

A.  S  =  {f | f(3)  =  f '(3)} 

B.  T  =  {f | f(0)f '(0)  =  0} 

  Solution

Problem 3

Let  S  =  {t², t² + 2t, t² + 3}  and T  =  {2t - 1, 5t - 3, t²} be subsets of P₂ 

A.     Prove that S is a basis for P₂.  

Solution

B.     Find the transition matrix P_S<--T.

Solution

Problem 4  

Suppose that you want to change the graphic file from the one on the left to the one on the right.  What is the matrix needed to adjust the pixels appropriately?  Assume the center of the picture is the origin.

                      
 Solution

Problem 5 

Let

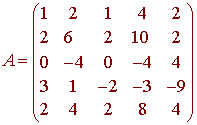
A.     Find the rank and the nullity of A. 

B.     Find a basis for the Null Space of A.

C.     Find a basis for the Column Space of A using columns of A.

D.     Find a basis for the Row Space of A using rows of A.

Solution

Problem 6

Let  S  =  {v₁, v₂, ..., v_n} be a set of linearly independent vectors and let v be a vector in the span of S.  Prove that v can uniquely be written as a linear combination of elements of S.  That is that prove that if

      v  =  a₁v₁ +a₂v₂ + ... + a_nv_n        and        v  =  b₁v₁ +b₂v₂ + ... + b_nv_n     

then

        a₁  =  b₂, a₂  =  b₂, ... , a_n  =  b_n

Solution