MATH 203 PRACTICE
EXAM I
Please work out each of the given problems. Credit will be based on the steps that you show towards the final answer. Show your work.
Problem 1
Let L: R2 → R3 be a linear transformation such that
L
(1,4) = (1,-1,3)
and L
(0,2) = (2,1,4)
Find L(1,0)
Solution
The key to this is to find the coordinates of (1,0) with respect to the basis (1,4) and (0,2). This is given by A-1(1,0)T .We have
![Matrix[(1,0),(4,2)]^-1 = Matrix[(1,0),(-2,1/2)]](img5.gif)
Multiplying, gives the coordinates (1,-2). Thus
L(1,0) = L[1(1,4) - 2(0,2)]
= L(1,4) - 2L(0,2)
= (1,-1,3) + 2(2,1,4)
= (5,1,11)
Problem 2
Suppose that you want to
change the graphic file from the one on the left to the one on the right.
What is the matrix needed to adjust the pixels appropriately?
Assume the center of the picture is the origin.


Solution
This is a reflection across the y-axis. The corresponding matrix is
![A = Matrix[(-1,0),(0,1)]](img8.gif)
Problem 3 For each of the two subsets below, determine if it is a subspace of Rn. If it is a subspace prove that it is. If it is not a subspace prove that it is not.
- {(x,y,z) in R3 | x - yz = 0}
- {(x,y,z,w) in R4 | x + 2y = z - w}
Solution
First, A. is not a subspace since (4,2,2) is in the set (4 - (2)(2) = 0), but 2(4,2,2) = (8,4,4) is not in the set (8 - (4)(4) = -8 is not 0).
For B. we need to prove the two statements. Note that a vector in this set is defined by z = x + 2y + w.
1. If u = (a,b,a+2b+c,c) and v = (d,e,d+2e+f), then
u+v = (a+d,b+e,a+2b+c+d+2e+f,c+f) = (a+d,b+e,a+d+2(b+e)+c+f,c+f)
and the vector has the correct form
2. ku = k(a,b,a+2b+c,c) = (ka,kb,ka+2kb+kc,kc)
and this vector has the correct form. Therefore this is a subspace.
Problem 4
Answer the following true or false and
explain your reasoning.
A.
If A and B
are n x n matrices and AB
= 0, then either A
= 0 or B = 0.
Solution
False, Consider
![A = Matrix[(1,0),(0,0)], B = Matrix[(0,0),(0,1)]](imgD.gif)
B.
If A is a matrix with A2
= In then
either det(A) =
1 or det(A)
= -1.
Solution
True: det(A2) = det(AA) = det(A)det(A)
= [det(A)]2 and det(I) = 1.
If x = det(A), this gives
x2 = 1. So that
x = 1 or x =
-1.
C. If the columns of an mxn
matrix A form a basis for Rm,
then m = n.
Solution
True, since the dimension of Rm
is m, there must be m vectors in any basis. Thus
the basis that consists of the columns must have m
vectors, meaning there are m columns: m = n.
D. If the nullity of an 8x11
matrix A is 6 then the
column space of A is a 5
dimensional subspace of R8.
Solution
True, the dimension of the column space is the rank of
A. We have:
Nullity + Rank = n
6 + Rank = 11
Rank = 5.
E. If the second column of a 4x4
matrix A does not contain a pivot, then
A is not invertible.
Solution
True, if the second column does not contain a pivot, then by TFAE,
A is not invertible.
F. If (1,3,4,1)T and
(2,5,0,6)T are both solutions of
Ax = b, then the equation
Ax = 0 has a nontrivial solution.
Solution
True. If u = (1,3,4,1)T
and v = (2,5,0,6)T, then
w = u-v is nontrivial,
and
Aw = A(u-v)
= Au - Av = b - b = 0.
Problem 5
Let
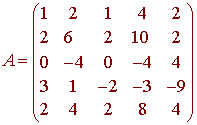
A.
Find the rank and the nullity of A.
Solution
The rank is equal to the number of pivots:
Rank A = 3.
The nullity is the number of
free variables or number of columns - Rank A = 2.
B.
Find a basis for the Null Space of A.
Solution
To find the null space you can put the
rref(A) into equation form to get:
x1 = 0, x2 = -x4
+ x5, x3 = -2x4 -4x5,
x4 = x4, x5 = x5
Now let x4 = 1 and
x5 = 0 to get
(0,-1,-2,1,0)
let x4 = 0 and
x5 = 1 to get (0,1,-4,0,1)
These two vectors form a basis for the null space of
A.
C.
Find a basis for the Column Space of A.
Solution
A basis for the Column
Space of A can be found by using the columns of
A that are pivots of A.
From rref(A), we see that the first three
columns have pivots. So the basis for the Column
Space of A is (1,2,0,3,2)T,
(2,6,-4,1,4)T, and
(1,2,0,-2,2)T.
Problem 6
v = a1v1
+a2v2 + ... + anvn
and
v
= b1v1
+b2v2 + ... + bnvn
then
a1 = b2, a2 = b2,
... , an = bn
Solution
Suppose that
v = a1v1
+a2v2 + ... + anvn
and
v
= b1v1
+b2v2 + ... + bnvn
Now subtract the two equations to get:
v - v = a1v1 +a2v2 + ... + anvn - (b1v1 +b2v2 + ... + bnvn )
Combine like terms to get
0 = (a1 - b1)v1 + (a2 - b2)v2 + ... + (an + bn)vn
Now since S is linearly independent we have by definition that
a1 - b1 = 0, + a2 - b2 = 0, ... , an + bn = 0
And the result follows.
Problem 7 Use the definition of span to prove that the vectors shown below span R2.
v = (3,5) and w = (2,3)
Solution
Let b = (b1,b2) be a vector in R2. We need to show that there is a solution to
x1v + x2w = bor that
x1(3,5) + x2(2,3) = (b1,b2)
This can be written as the matrix equation
![Matrix[(3,2),(5,3)] Matrix[x1,x2] = Matrix[b1,b2]](img4F.gif)
This has a solution since rref(A) is the identity element, so the inverse exists and the solution is x = A-1b.
Problem 8
Prove that if
v
and
w are solutions to the matrix equation Ax
=
b and if r + s = 0, then
rv +
sw
is a solution to the homogeneous equation Ax
= 0.
Solution
We have
A(rv + sw) = A(rv) = A(sw) = rAv + sAw
Since v and w are solutions to Ax = b, both Av and Aw are b. We get that the above equals
rb + sb = (r+s)b = 1b = b
Problem 9
As a consultant for the South Tahoe ski marketing group, your task is to make predictions on the ski pass that locals hold. You found that this year 55% of locals hold a pass for Heavenly, 30% hold a pass for Sierra-at-Tahoe, and 15% hold a pass for Kirkwood. Each year, 20% of the Heavenly pass holders defect to Sierra-at-Tahoe and 5% defect to Kirkwood. 10% of the Sierra-at-Tahoe pass holders defect to Heavenly and 20% defect to Kirkwood. 5% of the Kirkwood pass holders defect to Heavenly and 25% defect to Sierra-at-Tahoe. Assume that every pass holder remains a pass holder the following year and that everyone holds exactly one pass. Determine what the distribution of pass holders will be in five years.
Solution: We get the matrix:
![A = Matrix[(.75,.10,.05),(.20,.70,.25),(.05,.20,.70)]](img58.jpg)
Since we want to find the distribution after five years we take
![A^5 * Matrix[.55,.30,.15] = Matrix[.29,.42,.29]](img59.jpg)
So after 5 years, 29% will have Heavenly pass, 42% will have a Sierra-at-Tahoe pass, and 29% will have a Kirkwood pass.
Problem 10
Use the definition to find the determinant of the following matrix. Do not use your calculator.
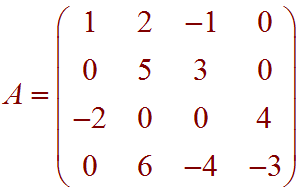
Expand by the second row. Note that since the first and last entry of the second row are both 0, we only need the middle numbers.
![5*Matrix[(1,-1,0),(-2,0,4),(0,-4,-3)] - 3*Matrix[(1,2,0),(-2,0,4),(0,6,-3)]](img5D.jpg)
Now expand each of these by their first rows to get
![5[Matrix[(0,4),(-4,-3)]+Matrix[(-2,4),(0,-3)]-3[Matrix[(0,4),(6,-3)] - 2*Marix[(-2,4),(0,-3)]]](img61.jpg)
= 5[16 + 6] - 3[-24 -12] = 110 + 108 = 218.
Extra Credit:
Write
down one thing that your instructor can do to make the class better and one
thing that you want to remain the same in the class.
(Any constructive remark will be worth full credit.)