MATH 203 PRACTICE MIDTERM I  

Printable Key

Part 1

Please work out each of the given problems without the use of a calculator.  Credit will be based on the steps that you show towards the final answer.  Show your work. 

Problem 1

Consider the matrix

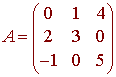
1. Use the definition of the determinant to find |A|.  
   Solution
2. Find the adjoint of A  
   Solution
3. Use the adjoint formula and parts A. and B. to find the inverse of A.  
   Solution

Problem 2

Let

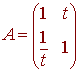
1. Find A² and A³.  
   Solution
2. Make a conjecture about A^k.  
   Solution
3. Use induction to prove your conjecture from part B.  
   Solution

Problem 3 

Let 

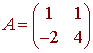
Find a 2x1 matrix v such that Av = 2v.

Part 2

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work. 

Problem 4 

Answer the following true or false and explain your reasoning.

A.     If A and B are n x n matrices and AB  =  0, then either A = 0 or B = 0.
Solution

B.     If A is a matrix with A²  =  I_n then either det(A)  =  1 or det(A)  =  -1.  
Solution

Problem 5 

Let v  =  [1   –2   1   2] ^T represent a sample of a function of four equispaced points. 

A.     Determine the final average and detail coefficients by computing.  A₂A₁v.  
Solution

B.     Using a threshold of e  =  1 determine the compressed data and then compute the wavelet.  
Solution

Problem 6 

In the city of Digraphville, there are four food-processing plants:  the apple plant, the beet plant, the carrot plant, and the dairy plant.  There are one-way roads from the apple plant to the beet plant and to the dairy plant.  There is also a one-way road from the beet plant to the carrot plant.  There are two-way roads from the apple plant to the carrot plant, from the beet plant to the dairy plant and from the carrot plant to the dairy plant.

A.     Sketch the digraph for this situation.
Solution

B.     Write down the adjacency matrix.
Solution

C.     Use the adjacency matrix to determine how many ways are there to drive from the apple plant to the dairy plant using no more than four roads counted with multiplicity.  
Solution

Problem 7 

Prove that if A, B, and C are n x n matrices, then

        A(B + C)  =  AB + AC

  Solution

Problem 8 

Prove that if v and w are solutions to the matrix equation Ax = b and if r + s = 0, then

rv + sw is a solution to the homogeneous equation Ax = 0.

  Solution

Extra Credit:  Write down one thing that your instructor can do to make the class better and one thing that you want to remain the same in the class.

(Any constructive remark will be worth full credit.)