Math 203 Practice Final Exam Printable Key

 

Please work out all of the following problems.  Credit will be given based on the progress that you make towards the final solution.  Show your work.  No calculators allowed for this page.

 

Problem 1 

Let

       

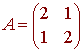
 Find an orthogonal matrix P and a diagonal matrix D with A  =  PDP-1.

Solution

We find

       

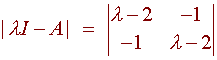
        =  (l - 2 )(l - 2) - 1  =  l2 - 4l + 3  =  (l - 1)(l - 3)

Hence the eigenvalues are 1 and 3.  Now we find the eigenvectors by finding the null space of A - lI.  We have

       

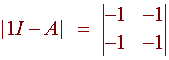
since the determinant is zero, we can use the first row which corresponds with the equation

        -x - y  =  0.

Which has eigenvector

        (1,-1)

Normalizing gives

        (1/ , -1/ )

For the eigenvector corresponding with the eigenvalue of 3, we have

       

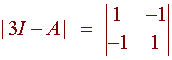
again, since the determinant is zero, we can use the first row which corresponds with the equation

        x - y  =  0.

Which has eigenvector

        (1,1)

Normalizing gives

        (1/ , 1/ )

Putting this all together, gives

       

 

 

Problem 2

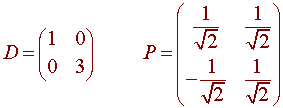
Use the permutation definition of the determinant to find the determinant of  

       

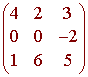
Solution

The permutations on three elements and their corresponding products are

          even             odd           odd            even           even          odd
        (1,2,3)         (1,3,2)       (2,1,3)        (2,3,1)        (3,1,2)      (3,2,1)

        (4)(0)(5) - (4)(-2)(6) - (2)(0)(5) + (2)(-2)(1) + (3)(0)(6) - (3)(0)(1)

          =  48 - 4  =  44

 

Problem 3

Find the inverse of A if

         

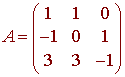
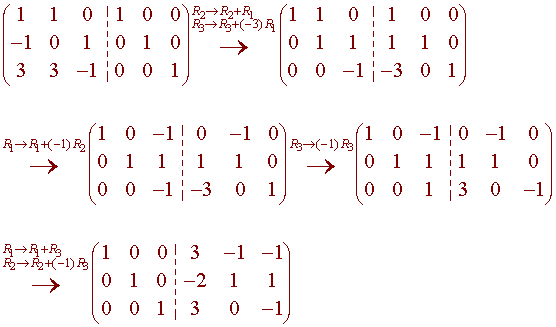
  We augment this matrix with the identity matrix and rref it.

               

We conclude that

       


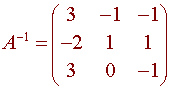
Calculators are permitted on this part

 

Problem 4

Consider the matrix

 

          

 

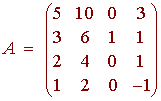
A.     Determine the rank of A.

Solution

We find

       

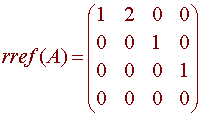
Since there are three corners, the rank is 3.

B.   Find a basis for the null space of A.

Solution

The equation form of rref(A) is

                x1  =  -2x2        
          x2  =  x2 
          x3  =  0
          x4  =  0

Since the rank of A is 3 and n  =  4, the nullity is 1.  A basis for the null space is

        {(-2, 1,0,0)}

C.     Find a basis for the column space of A using columns of A.

Solution

We see that the corners are in columns 1, 3, and 4.  Hence the first, second, and third columns of A are a basis for the column space of A.  

        {(5,3,2,1), (0,1,0,0), (3,1,1,-1)}

 

 

Problem 5       Let    be defined by

       

 

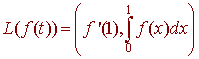
A.    Prove that L is a linear transformation.

Solution

Let 

        f(t)  =  a1 + b1t + c1t2        and        g(t)  =  a2 + b2t + c2t2  

Then 

     1.     L(f(t) + g(t))  =  (b1 + 2c1 + b2 + 2c2, a1 + 1/2 b1 + 1/3 c1 + a2 + 1/2 b2 + 1/3 c2)     

             and

            L(f(t)) + L(g(t))  =  (b1 + 2c1, a1 + 1/2 b1 + 1/3 c1) + (b2 + 2c2, a2 + 1/2 b2 + 1/3 c2)

            =  (b1 + 2c1 + b2 + 2c2, a1 + 1/2 b1 + 1/3 c1 + a2 + 1/2 b2 + 1/3 c2)     

    2.  L(cf(t))  =  (cb1 + 2cc1, ca1 + 1/2 cb1 + 1/3 cc1)  =  c(b1 + 2c1, a1 + 1/2 b1 + 1/3 c1)  =  cL(f(t))

hence L is a linear transformation

B.   Let S = {x2 + x, x2 + 1, x} and T = {(1,1), (1,2)} be bases for P2 and R2.  Find the matrix for L with the bases S and T. 

Solution
We find

               

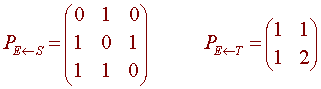
    and

        L(1,0,0)  =  L(1)  =  (0,1)

        L(0,1,0)  =  L(t)  =  (1,1/2)

        L(0,0,1)  =  L(t2)  =  (2,1/3)

Hence

           

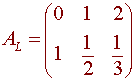
Now consider the diagram

       

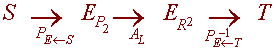
We the matrix we want is

       

 

Problem 6 

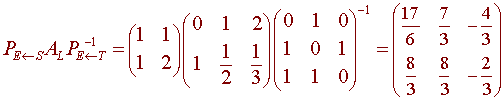
Show that the set

       

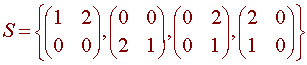
is a basis for M2x 2.

Solution

Since there are four vectors in a four dimensional space, we only need to show that the vectors are linearly independent.  We let

         

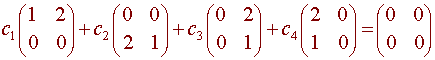
This gives us the four equations 

        c1 + 2c4  =  0
        2c1 + 2c3  =  0
        2c2 + c4  =  0
        c2 + c3  =  0

Putting this into the matrix form Ac  =  0 gives

       

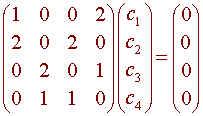
We calculate 

        |A|  =  -6

Since the determinant is nonzero, the above equation has only the trivial solution.  Hence the four vectors are linearly independent.  We can conclude that they form a basis for M2x2.

Problem 7 Use matrices to find the unknown currents in the given circuit.

         

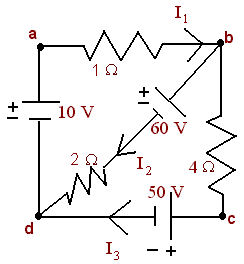
Solution

First we find the loop equations.

        a -->  b -->  d -->  a :    -I1 - 60 - 2I2 + 10  =  0

        b -->  c -->  d -->  b :    -4I3 - 50 + 2I2 + 60  =  0

  The node equations are 

        b:  I1 - I2 - I3  =  0

        d:  -I1 + I2 + I3  =  0

Notice that the second node equation is redundant, so we can discard this one.  The three equations together give

  

        -I1 - 2I2  =  50

         2I2 - 4I3  =  -10

         I1 - I2 - I3  =  0

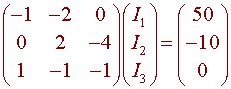
  The corresponding matrix equation AI  =  b is

       

Hence, the solution is I  =  A-1b.  We have

       

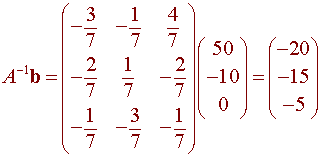
so that

         I1  =  -20         I2  =  -15        I3  =  -5

Notice that the minus signs means that the currents are traveling in the opposite direction as the arrows indicate.

 

Problem 8

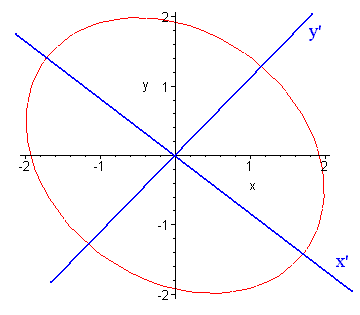
Graph the equation and write the equation in standard form.

        4x2 + 2xy + 4y2  =  15

  Solution

We first write this as a matrix equation xTAx  =  15.

       

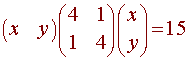
  Next we find the eigenvalues of this matrix.  They are 3 and 5.  We used a calculator for this, but we could have done this by hand.  We have

       

The eigenvectors are

       

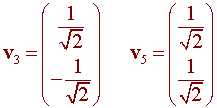
The equation can be written in the form xTPDPTx  =  15

       

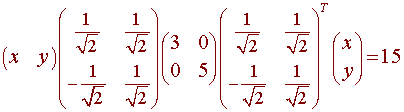
Let

        x'  =  PTx 

Then the equation of the conic becomes

        x'TDx'  =  15

or

        3x'2 + 5y'2  =  15

or

            x'2        y'2  
                  +            =  15
            5         3

We see that the graph is rotated from the (x,y) plane by an angle of 

        arctan(-1)  =  -p/4

The graph is shown below.

       

 

 

Problem 9

One of the following is a subspace of the space of differentiable functions. 

            I.   {f | f(0) – f '(0)  =  1}          II. {f | f(1)  =  f '(1)} 

 

A.     Determine which is not a subspace and explain why.

Solution

The first one is not a subspace.  For example f(x)  =  -x is in the set, but 2f(x)  =  -2x is not.

B.     Prove that the other one is a subspace.

      Solution

        If f(1)  =  f '(1) and g(1)  =  g '(1) then

        (f + g)(1)  =  f(1) + g(1)  =  f '(1) + g'(1)  =  (f + g)'(1)

        proving closure under "+".  Also

        (cf)(1)  =  c(f(1))  =  c(f '(1))  =  (cf)'(1)

        proving closure under " . "  Hence set II is a subspace of the space of differentiable functions.

Problem 10

Prove that if A is a matrix such that A2 = 0 then 0 is an eigenvalue for A.

  Solution

We need to show that there is a nonzero v with 

        Av  =  0v  =  0

This is true if and only if 

        det(A)  =  0

but 

        (det A)2  =  det(A2)  =  det(0)  =  0

hence det A  =  0, and we can conclude that 0 is an eigenvalue for A.

Problem 11

Answer the following true or false. If it is true, explain why.  If it is false explain why or provide a counter example.

A.    If S  =  {v1, v2} is a linear independent set of vectors in R3 and v3 is not in the span of S, then  {v1, v2, v3} is a basis for R3.

 Solution

            True, since then dim(Span{v1, v2, v3})  > dim(Span(S))  =  2.  Hence dim(Span{{v1, v2, v3}} = 3.  Since any 3 vectors in R3 is a basis for R3.

 

B.     Every orthonormal set of five vectors in R5 is a basis for R5.

Solution

True, since orthonormal vectors are always linearly independent and five linearly independent vectors in R5 always form a basis for R5.

C.     Let A and B be matrices such that A2v = a, B2v = b, and ABv = c.  Then

(A + B)2 v  =  a + b + 2c

Solution

False,

(A + B)2v  =  (A2 + AB + BA + B2)v  =  A2v + ABv + BAv + B2v  =  a + b + c + BAv

So as long as ABv is not equal to BAv, the statement is false.  Remember that matrix multiplication does not enjoy the commutative property.