Please work out all of the following problems. Credit will be
given based on the progress that you make towards the final solution. Show
your work. No calculators allowed for this page.
Problem 1
Let
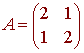
Find
an orthogonal matrix P and a diagonal matrix D
with A =
PDP-1.
Problem 2
Use the definition of the
determinant to find the determinant of
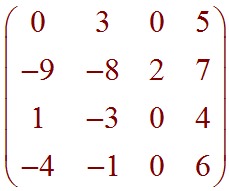
Problem 3
Find the inverse of A
if
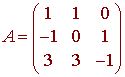
Calculators are permitted on this part
Problem 4
Consider the matrix
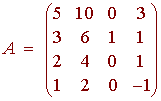
A.
Determine the rank of A.
B.
Find a basis for the null space of A.
C.
Find a basis for the column space of A using
columns of A.
Problem 5
Let
![]() be defined by
be defined by
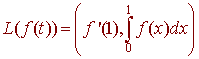
A.
Prove
that L is a linear transformation.
B. Let S = {x2 + x, x2 + 1, x} and T = {(1,1), (1,2)} be bases for P2 and R2. Find the matrix for L with the bases S and T.
Problem 6
Show that the set
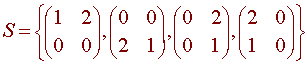
is a basis for M2x
Problem 7 Use matrices to find the unknown currents in the given circuit.
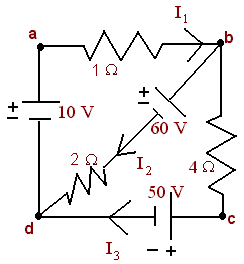
Problem 8
Graph the equation and write the equation in
standard form.
4x2 + 2xy + 4y2
= 15
Problem 9
One of the
following is a subspace of the space of differentiable functions.
I. {f | f(0) – f ‘(0)
= 1}
II. {f
| f(1) =
f ‘(1)}
A.
Determine which is not a subspace
and explain why.
B.
Prove
that the other one is a subspace.
Problem 10
Prove that if A
is a matrix such that A2 = 0 then 0
is an eigenvalue for A.
Problem 11
Answer the following true or false. If it is
true, explain why. If it is false
explain why or provide a counter example.
A. If S = {v1, v2} is a linearly independent set of vectors in R3 and v3 is not in the span of S, then {v1, v2, v3} is a basis for R3.
B.
Every orthonormal set of five vectors in R5
is a basis for R5.
C.
Let A and B be
matrices such that A2v = a, B2v
= b, and ABv = c.
Then
(A
+ B)2 v = a + b + 2c
D. If T is a 1-1 linear transformation from P3 to M2x2, then {T(1), T(1+t), T(1+t2), T(1+t3)} is a basis for M2x2.
E. There exists a matrix A that is diagonalizable but not orthogonally diagonalizable.
F. If the determinant of a matrix A is greater than 1, then ||Ax|| > ||x|| for all nonzero vector x.