Please work out all of the following problems. Credit will be
given based on the progress that you make towards the final solution. Show
your work. No calculators allowed for this page.
Let
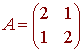
Find
an orthogonal matrix P and a diagonal matrix D
with A =
PDP-1.
Solution
We find
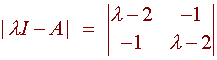
= (l - 2 )(l - 2) - 1 = l2 - 4l + 3 = (l - 1)(l - 3)
Hence the eigenvalues are 1 and 3. Now we find the eigenvectors by finding the null space of A - lI. We have
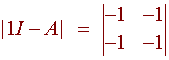
since the determinant is zero, we can use the first row which corresponds with the equation
-x - y = 0.
Which has eigenvector
(1,-1)
Normalizing gives
(1/![]() , -1/
, -1/![]() )
)
For the eigenvector corresponding with the eigenvalue of 3, we have
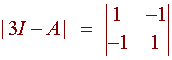
again, since the determinant is zero, we can use the first row which corresponds with the equation
x - y = 0.
Which has eigenvector
(1,1)
Normalizing gives
(1/![]() , 1/
, 1/![]() )
)
Putting this all together, gives
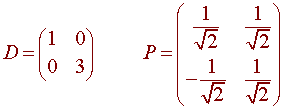
Use the permutation definition of the
determinant to find the determinant of
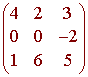
Solution
The permutations on three elements and their corresponding products are
even
odd
odd
even
even odd
(1,2,3)
(1,3,2)
(2,1,3)
(2,3,1)
(3,1,2) (3,2,1)
Find the inverse of A
if
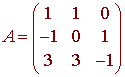
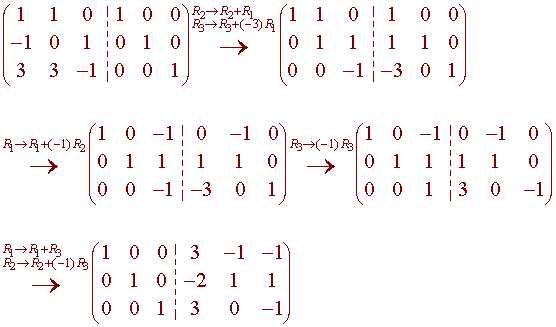
We conclude that
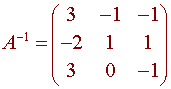
Calculators are permitted on this part
Problem 4
Consider the matrix
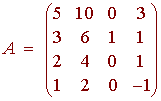
A. Determine the rank of A.
Solution
We find
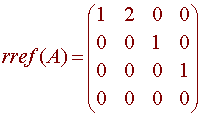
Since
there are three corners, the rank is 3.
B. Find a basis for the null space of A.
Solution
x1 = -2x2
x2
= x2
x3
= 0
x4
= 0
Since the rank of A is 3 and n = 4, the nullity is 1. A basis for the null space is
{(-2, 1,0,0)}
C.
Find a basis for the column space of A using
columns of A.
Solution
We see that the corners are in columns 1, 3, and 4. Hence the first, second, and third columns of A are a basis for the column space of A.
{(5,3,2,1), (0,1,0,0), (3,1,1,-1)}
Problem 5
Let
![]() be defined by
be defined by
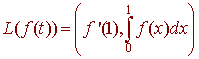
A.
Prove that L is
a linear transformation.
Let
f(t) = a1 + b1t + c1t2 and g(t) = a2 + b2t + c2t2
Then
1. L(f(t) + g(t)) = (b1 + 2c1 + b2 + 2c2, a1 + 1/2 b1 + 1/3 c1 + a2 + 1/2 b2 + 1/3 c2)
and
L(f(t)) + L(g(t)) = (b1 + 2c1, a1 + 1/2 b1 + 1/3 c1) + (b2 + 2c2, a2 + 1/2 b2 + 1/3 c2)
= (b1 + 2c1 + b2 + 2c2, a1 + 1/2 b1 + 1/3 c1 + a2 + 1/2 b2 + 1/3 c2)
2. L(cf(t)) = (cb1 + 2cc1, ca1 + 1/2 cb1 + 1/3 cc1) = c(b1 + 2c1, a1 + 1/2 b1 + 1/3 c1) = cL(f(t))
hence L is a linear transformation
B. Let S = {x2 + x, x2 + 1, x} and T = {(1,1), (1,2)} be bases for P2 and R2. Find the matrix for L with the bases S and T.
Solution
We find
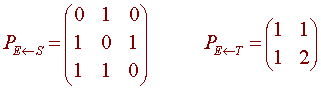
and
L(1,0,0) = L(1) = (0,1)
L(0,1,0) = L(t) = (1,1/2)
L(0,0,1) = L(t2) = (2,1/3)
Hence
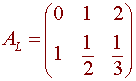
Now consider the diagram
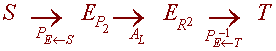
We the matrix we want is
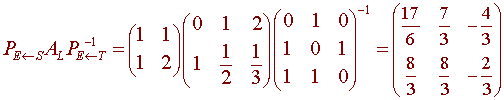
Show that the set
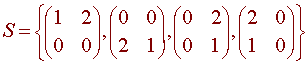
is a basis for M2x
Solution
Since there are four vectors in a four dimensional space, we only need to show that the vectors are linearly independent. We let
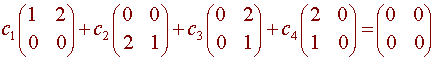
This gives us the four equations
c1 + 2c4 = 0
2c1 + 2c3
= 0
2c2 + c4
= 0
c2 + c3
= 0
Putting this into the matrix form Ac = 0 gives
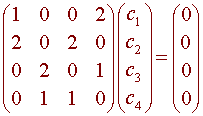
We calculate
|A| = -6
Since the determinant is nonzero, the above equation has only the trivial solution. Hence the four vectors are linearly independent. We can conclude that they form a basis for M2x2.
Problem 7 Use matrices to find the unknown currents in the given circuit.
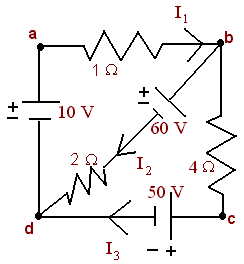
Solution
First we find the loop equations.
a --> b --> d --> a : -I1 - 60 - 2I2 + 10 = 0
b --> c --> d --> b : -4I3 - 50 + 2I2 + 60 = 0
b: I1 - I2 - I3 = 0
d: -I1 + I2 + I3 = 0
Notice that the second node equation is redundant, so we can discard this one. The three equations together give
-I1 - 2I2 = 50
2I2 - 4I3 = -10
I1 - I2 - I3 = 0
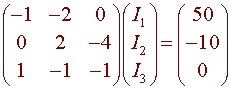
Hence, the solution is I = A-1b. We have
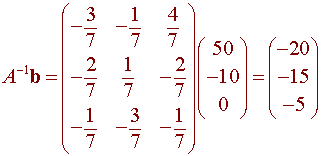
so that
I1 = -20 I2 = -15 I3 = -5
Notice that the minus signs means that the currents are traveling in the opposite direction as the arrows indicate.
Problem 8
Graph the equation and write the equation in
standard form.
4x2 + 2xy + 4y2
= 15
We first write this as a matrix equation xTAx = 15.
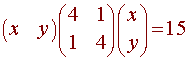

The eigenvectors are
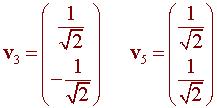
The equation can be written in the form xTPDPTx = 15
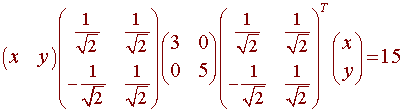
Let
x' = PTx
Then the equation of the conic becomes
x'TDx' = 15
or
3x'2 + 5y'2 = 15
or
x'2 y'2
+
= 15
5 3
We see that the graph is rotated from the (x,y) plane by an angle of
arctan(-1) = -p/4
The graph is shown below.
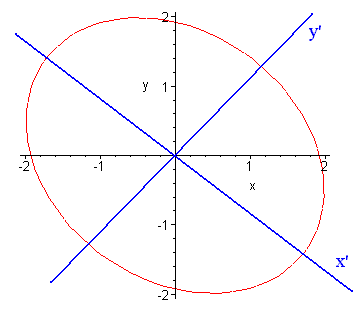
Problem 9
One of the
following is a subspace of the space of differentiable functions.
I. {f | f(0) – f '(0)
= 1}
II. {f
| f(1) =
f '(1)}
A. Determine which is not a subspace and explain why.
Solution
B.
Prove
that the other one is a subspace.
If f(1) = f '(1) and g(1) = g '(1) then
(f + g)(1) = f(1) + g(1) = f '(1) + g'(1) = (f + g)'(1)
proving closure under "+". Also
(cf)(1) = c(f(1)) = c(f '(1)) = (cf)'(1)
proving closure under " . " Hence set II is a subspace of the space of differentiable functions.
Problem 10
Prove that if A
is a matrix such that A2 = 0 then 0
is an eigenvalue for A.
We need to show that there is a nonzero v with
Av = 0v = 0
This is true if and only if
det(A) = 0
but
(det A)2 = det(A2) = det(0) = 0
hence det A = 0, and we can conclude that 0 is an eigenvalue for A.
Problem 11
Answer the following true or false. If it is
true, explain why. If it is false
explain why or provide a counter example.
A.
If S
= {v1,
v2}
is a linear independent set of vectors in R3
and v3 is not in the span of S,
then {v1,
v2, v3}
is a basis for R3.
True, since then dim(Span{v1, v2, v3}) > dim(Span(S)) = 2. Hence dim(Span{{v1, v2, v3}} = 3. Since any 3 vectors in R3 is a basis for R3.
B. Every orthonormal set of five vectors in R5 is a basis for R5.
Solution
True, since orthonormal
vectors are always linearly independent and five linearly independent vectors in
R5 always form a basis for R5.
C.
Let
A and
B be
matrices such that
A2v = a, B2v
= b, and
ABv = c.
Then
(A + B)2 v = a + b + 2c
Solution
False,
(A + B)2v = (A2 + AB + BA + B2)v = A2v + ABv + BAv + B2v = a + b + c + BAv
So as long as ABv is not equal to BAv, the statement is false. Remember that matrix multiplication does not enjoy the commutative property.