Math 203 Practice
Please work out each
of the given problems. Credit will
be based on the steps towards the final answer.
Show your work. Do your work
on your own paper.
Let S
= {t2, t2 + 2t, t2 + 3}
and T
= {2t - 1, 5t - 3, t2}
be subsets of P2
A. Prove that S is a basis for P2.
Solution
Since the dimension of P2 is 3 and S has 3 vectors, we need only prove that the vectors in S are linearly independent. If we let
c1t2 + c2(t2 + 2t) + c3(t2 + 3) = 0
then we can combine like terms to obtain
(c1 + c2 + c3)t2 + 2c2t + 3c3 = 0
If a polynomial equals zero then each of the coefficients equal zero. We get
c1
+ c2 + c3 = 0
2c2
= 0
3c3 = 0
The matrix for this equation is
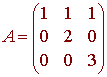
has determinant equal to 6. Since the determinant is nonzero, the system has only the trivial solution, hence the three vectors are linearly independent. We can conclude that S is a basis for P2.
B. Find the
change of basis
matrix PS<--T
.
Solution
Let E be a standard basis E = {t2, t, 1} and look at the following diagram
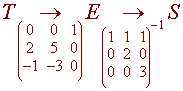
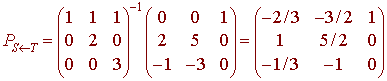
Of the following two
subsets of the vector space of differentiable functions, determine which is a
subspace. For the one that is not a
subspace, demonstrate why it is not. For
the one that is a subspace, prove that it is a subspace.
A.
S = {f | f(3) = f '(3)}
B.
T = {f | f(0)f '(0) = 0}
Solution
A. This is a subspace. We need to show that the two closure properties hold.
f(3) = f '(3) and g(3) = g'(3)
then
(f + g)(3) = f(3) + g(3) = f '(3) + g'(3) = (f + g)'(3)
hence f + g is in the subset. If c is a constant, then
(cf)(3) = cf(3) = cf '(3) = (cf)'(3)
hence cf is in the subset. Since both closure properties are true, we can conclude that S is a subspace.
B. This set is not a subspace. Let f(t) = 1 and g(t) = t. Then
f(0)f '(0) = (1)(0) = 0 and g(0)g'(0) = (0)(1) = 0
so both f and g are in T. However
(f + g)(0)(f + g)'(0) = [f(0) + g(0)] [f '(0) + g'(0)] = (1 + 0)(0 + 1) = 1
Hence T is not closed under addition.
Let
V be the subspace of differentiable functions
spanned by {ex, e2x, e3x}
and let
L: V
---> V
be the linear transformation with
L(f(x)) = f ''(x) - 3f '(x) + 2f(x)
A.
Write down the matrix AL with
respect to the given basis.
Solution
We have
L((1,0,0) = L(ex) = ex - 3ex + 2ex = 0 = (0,0,0)
L((0,1,0) = L(e2x) = 4e2x - 6e2x + 2e2x = 0 = (0,0,0)
L((0,0,1) = L(e3x) = 9e3x - 9e3x + 2e3x = 2e3x = (0,0,2)
The matrix of L is the matrix whose columns are the vectors above.
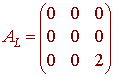
B.
Find the a basis for the kernel and range of L.
A basis for the kernel corresponds to the null space of AL which has basis
{(1,0,0), (0,1,0)}
in other words the basis is given by
{ex, e2x}
Problem 4
Let W
= Span{(1,1,0,1), (0,1,2,3)}. Find
a basis for the orthogonal complement of W.
The orthogonal complement is equal to the null space of the matrix whose rows are the given vectors. If
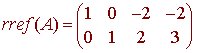
then the rref(A) is given by
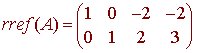
so that a basis for the null space is given by
{(2,-2,1,0), (2,-3,0,1)}
Problem 5
Let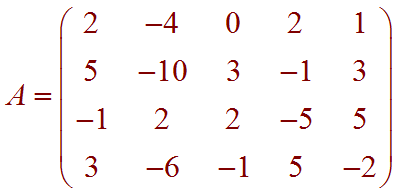
Find the following:
Solution
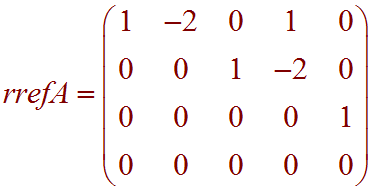
-
A basis for the column space of A.
Solution: The pivots are in columns 1 and 3, so the first and third rows of A are a basis for Col A.
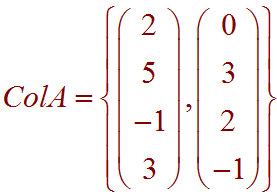
-
A basis for the row space of A.
Solution: A basis for the row space consists of the pivot rows of rrefA.
RowA = {(1,-2,0,1,0), (0,0,1,-2,0), (0,0,0,0,1)} -
A basis for the null space of A.
Solution: First turn the rrefA into equation form:
x1 - 2x2 + x4 = 0
x2 = x2
x3 - 2x4 = 0
x4 = x4
x5 = 0
The free variables are x2 and x4, so send these to the right hand side and call them s and t respectively.
x1 = 2s - t
x2 = s
x3 = 2t
x4 = t
x5 = 0
Finally, we can find a basis by first setting (s,t) = (1,0) and then (s,t) = (0,1) to get the basis vectors.
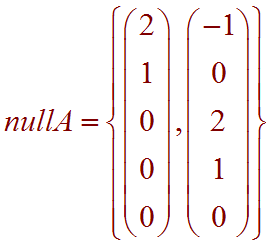
-
The nullity of A.
Solution: The nullity of a matrix is just the number of vectors in a basis for the null space. So the nullity is 2. -
The rank of A.
Solution: The rank of a matrix is just the number of vectors in a basis for the row space (or column space). So the rank is also 2.
Problem 6
Let L: V ---> V be a linear transformation. Use the fact that
dim(Ker L) + dim(Range L) = dim(V)
to show that if L
is one to one then L is onto.
Solution
dim(Ker L) = 0
The equation tells us that
dim(Range L) = dim(V)
Since the range is a subspace of V and has the same dimension as V, the range of L equal V. We can conclude that L is onto.
Problem 7
Let A
and B be matrices and let v
be an eigenvector of both A and B.
Prove that v
is an eigenvector of the product AB.
Proof
If v is an eigenvector of A and B, then there are numbers a and b with
Av = av and Bv = bv
We then have
(AB)v = A(Bv) = A(bv) = b(Av) = bav = abv
Hence v is an eigenvector of AB with eigenvalue ab.
![A = Matrix[ (2,6),(6,7)]](img9.gif)
Solution
First find the eigenvalues.
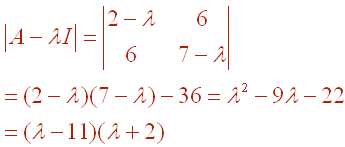
Thus l = 11 or l = -2
![Matrix[(-9,6),(6,-4)] gets rref to Matrix[(1,2/3),(0,0)]](img13.gif)
![Matrix[(4,6),(6,9)] rref to Matrix[(1,3/2),(0,0)]](imgD1.gif)
Thus the equations are: x = -3/2 y and y = y. Setting y = 2 gives the vector (-3,2).
The diagonal matrix has the eigenvalues on the diagonal:
![D = Matrix[(11,0),(0,2)]](imgF1.gif)
and the P matrix is the matrix with its columns as the eigenvectors.
![P = Matrix[[(2,-3),(3,2)]](img11.gif)
Finally, we just need the inverse of P. We use the adjoint formula.
![P^-1 = 1/13 Matrix[(2,3),(-3,2)] = Matrix[(2/13,3/13),(-3/13,2/13)]](img18.gif)
Problem 9
Answer True of False and
explain your reasoning.
A. Let A be a 3x3 matrix such that the columns of A form an orthonormal set of vectors. Then
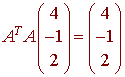
Solution
True, since A is an orthogonal matrix, we have
AT = A-1
so that
ATA = A-1A = I
B. B. If A is an mxn matrix such that the rows of A and the columns of A are both linear independent sets, then n = m.
True. Since the rows are linear dependent the dimension of the row space is m. Since the columns of A are linear independent, the dimension of the column space of A is n. But the row space and column space always have the same dimension. Thus m = n.
C. If u and v are eigenvectors for a matrix A, then u + v is also an eigenvector for A.
Solution
False. For example if Au = u and Av = 2v, then A(u+v) = Au + Av = u + 2v which is not a multiple of u+v.
D. If A is similar to B and B is similar to C, then A is similar to C.
Solution
True. Since A is similar to B, there is an invertible matrix P with A = PBP-1. Since B is similar to C, there is an invertible matrix R with B = RCR-1. Substituting gives
A = P(RCR-1)P-1 = (PR)C(R-1P-1) = (PR)C(PR)-1
which is in the correct form.
E. If l is an eigenvalue for A, then l2 is an eigenvalue for A2.
True. If v is the eigenvector corresponding to l, then
Av = lvso that
F. The vectors (1,1,0), (1,0,1), and (0,0,1) are a basis for P2.
False, for vectors to be a basis for a vector space, they must be in the vector space. (1,1,0) is not a polynomial.