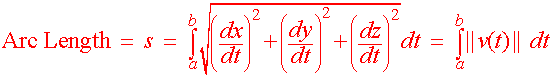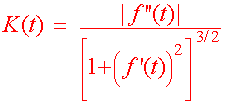Arc Length Curvature

Arc Length

For a parametrically defined curve we had the definition of arc length.  Since vector valued functions are parametrically defined curves in disguise, we have the same definition.  We have the added benefit of notation with vector valued functions in that the square root of the sum of the squares of the derivatives is just the magnitude of the velocity vector.  

 

Definition of Arc Length Let                 r(t)  =  x(t) i + y(t) j + z(t) k be a differentiable vector valued function on [a,b].  Then the arc length s is defined by

Example

Suppose that 

        r(t)  =  3t i + 2j + t²k

Set up the integral that defines the arc length of the curve from 2 to 3.  Then use a calculator or computer to approximate the arc length.

Solution

We use the arc length formula

Notice that we could do this integral by hand by letting t  =  9/2 tan q, however the question only asked us to use a machine to approximate the integral.  A TI 89 calculator gives

        s  =  5.8386

Parameterization by Arc Length

Recall that like parametric equations, vector valued function describe not just the path of the particle, but also how the particle is moving.  Among all representations of a curve there is a "simplest" one.  If the particle travels at the constant rate of one unit per second, then we say that the curve is parameterized by arc length.  We have seen this concept before in the definition of radians.  On a unit circle one radian is one unit of arc length around the circle.  When we say "simplest" we in no way mean that the equations are simple to find, but rather that the dynamics of the particle are simple.  To aid us in parameterizing by arc length, we define the arc length function.

 

Definition of the Arc Length Function If r(t) is a differentiable vector valued function, then the arc length function is defined by

Remark:  By the second fundamental theorem of calculus, we have

                    s'(t)  =  ||v(t)||

If a vector valued function is parameterized by arc length, then 

        s(t)  =  t

If we have a vector valued function r(t) with arc length s(t), then we can introduce a new variable 

        s  =  s^-1(t)

So that the vector valued function r(s) will have arc length equal to 

        s(s^-1(t))  =  t

so that r(s)  will be parameterized by arc length.  This process is usually impossible for two reasons.  Firstly, the integral that defines arc length involves a square root in the integrand.  This integral is usually impossible to determine.  Secondly, even if the integral is possible to evaluate, finding the inverse of a function is often impossible.  There are a few special curves that can be parameterized by arc length.  We will demonstrate one of them.

Example:     Parameterizing by arc length

Find the arc length parameterization of the helix defined by 

        r(t)  =  cos t i + sin t j + t k

Solution

First find the arc length function

Solving for t gives

        t   =  s /

Now substitute back into the position equation to get

        r(s)  =  cos(s / ) i + sin(s /) j + s / k

Definition of Curvature

Consider a car driving along a curvy road.  The tighter the curve, the more difficult the driving is.  In math we have a number, the curvature, that describes this "tightness".  If the curvature is zero then the curve looks like a line near this point.  While if the curvature is a large number, then the curve has a sharp bend.  

More formally, if T(t) is the unit tangent vector function then the curvature is defined at the rate at which the unit Tangent vector changes with respect to arc length.  

        Curvature = k = ||d/ds (T(t)) || =  ||r''(s)||

As we stated previously, this is not a practical definition, since parameterizing by arc length is typically impossible.  Instead we use the chain rule to get

         ||d/ds (T(t)) ||  =  ||T'(t) dt/ds|| 

                  ||T'(t)||              ||T'(t)||
          =                      =                      
                  ||ds/dt||              ||r'(t)||

This formula is more practical to use, but still cumbersome.  T'(t) is typically a mess.  Instead we can borrow from the formula for the normal vector to get the curvature

 

||r'(t) x r''(t)||      K(t)   =                                                     ||r'(t)||3

Example  

Find the curvature at p/2 if

        r(t) = cos t i - 1/t j + sin t k

Solution

We take derivatives

        r'(t)  =  -sin t i + 1/t² j + cos t k

        r''(t)  =  -cos t i - 2/t³ j - sin t k

Plugging in p/2 gives

        r'(p/2)  =  -i  +  4/p² j

        r''(p/2)  =  -16/p³ j - k 

Now take the cross product to get

        r'(p/2)  x  r''(p/2)  =  -4/p² i - j + 16/p³ k

Finally, we plug this information into the curvature formula to get

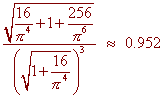
Curvature of a Plane Curve

If a curve in the xy-plane is defined by the function y = f(t) then there is an easier formula for the curvature.  We can parameterize the curve by 

        r(t)  =  t i + f(t) j 

We have

        r'(t)  =  i + f '(t) j 

        r''(t)  =  f ''(t) j 

Their cross product is just

        r'(t)  x  r''(t)  =  f ''(t) k

which has magnitude 

        ||r'(t)  x  r''(t)||  =  |f ''(t)|

The curvature formula gives

 

Curvature for a Plane Curve

Example

Find the curvature for the curve

        y  =  sin x

Solution

We have 

        f '(x)  =  cos x

        f ''(x)  =  -sin x

Plugging into the curvature formula gives

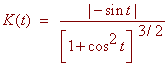
The Osculating Circle

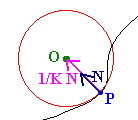
In first year calculus we saw how to approximate a curve with a line , parabola, etc.  Instead we can find the best fitting circle at the point on the curve.  If P is a point on the curve, then the best fitting circle will have the same curvature as the curve and will pass through the point P.  We will see that the curvature of a circle is a constant 1/r, where r is the radius of the circle.  The center of the osculating circle will be on the line containing the normal vector to the circle.  In particular the center can be found by adding

OP + 1/K N  

Exercise  

Find the equation of osculating circle to y = x² at x = -1.  

Solution

The Normal Component of Acceleration Revisited

How is the normal component of acceleration related to the curvature.  If you remember, the normal component the acceleration tells us how fast the particle is changing direction.  If a curve has a sharp bend (high curvature) then the directional change will be faster.  We now show that there is a definite relationship between the normal component of acceleration and curvature.

        a(t) = a_TT(t) + a_NN(t)

We have

        a(t) = r''(t) = d/dt(r'(t)) = d/dt(||r'(t)||T(t)) = d/dt(||r'(t)||)T(t) + ||r'(t)||T'(t)

        = s''(t)T(t) + s'T'(t) = s''(t)T(t) + s'||T'(t)||N(t) = s''(t)T(t) + ks^'2N(t)

So that the tangential component of the acceleration is s''(t) and the normal component is k(t)s^'2(t)  

Exercise

Find the tangential and normal components of

        r(t) = ti - 2tj + t²k

Back to the Vector Valued Functions Home Page

Back to the Vector Calculus Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions