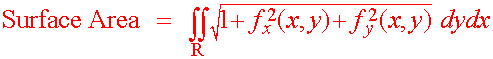Surface Area

Definition of Surface Area

In first year calculus we have seen how to find the surface area of revolution.  Now that we how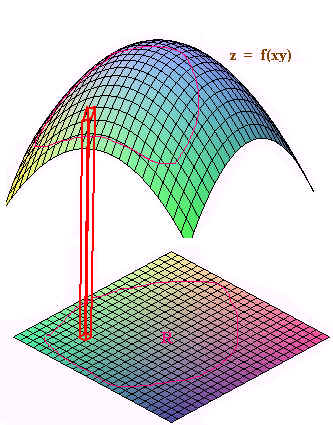 the power of double integration, we are ready to take on the surface area for more general surfaces.  We can think of a smooth surface as a quilt flapping in the wind.  It consists of many rectangles patched together.  More generally and more accurately, let z  =  f(x,y) be a surface in R³ defined over a region R in the xy-plane.  cut the xy-plane into rectangles.  Each rectangle will project vertically to a piece of the surface as shown in the figure below.  Although the area of the rectangle in R is 

        Area  =  DyDx

The area of the corresponding piece of the surface will not be DyDx since it is not a rectangle.  Even if we cut finely, we will still not produce a rectangle, but rather will approximately produce a parallelogram.  With a little geometry we can see that the two adjacent sides of  the parallelogram are (in vector form) 

        u  =  Dx i + f_x(x,y)Dx k 

and

        v  =  f_y(x,y)Dy i + Dy k 

We can see this by realizing that the partial derivatives are the slopes in each direction.  If we run Dx  in the i direction, then we will rise  f_x(x,y)Dx in the k direction so that

        rise/run  =   f_x(x,y)

Which agrees with the slope idea of the partial derivative.  A similar argument will confirm the equation for the vector v.  Now that we know the adjacent vectors we recall that the area of a parallelogram is the magnitude of the cross product of the two adjacent vectors.  We have

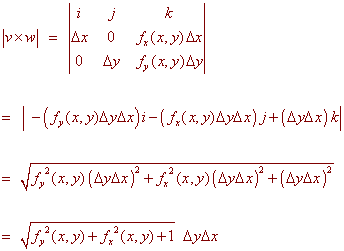
This is the area of one of the patches of the quilt.  To find the total area of the surface, we add up all the areas and take the limit as the rectangle size approaches zero.  This results in a double Riemann sum, that is a double integral.  We state the definition below.

Examples

Example

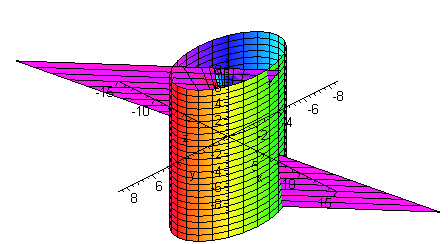
Find the surface area of the part of the plane 

        z  =  8x + 4y

that lies inside the cylinder

        x² + y²  =  16

Solution

We calculate partial derivatives

        f_x(x,y)  =  8            f_y(x,y)  =  4

so that 

        1 + f_x²(x,y)  + f_y²(x,y)  =  1 + 64 + 16  =  81

Taking a square root and integrating, we get 

We could work this integral out, but there is a much easier way.  The integral of a constant is just the constant times the area of the region.  Since the region is a circle, we get

        Surface Area  =  9(16p)  =  144p 

In reality, since there is a square root in the formula, most surface area calculations require intensive integration skills or the use of a machine.  The prior example and the next example are not meant to deceive, but rather to show how the essence of surface area problems work without the integration difficulty clouding your understanding.

Example

Find the surface area of the part of the paraboloid 

        z  =  25 - x² - y² 

that lies above the xy-plane.

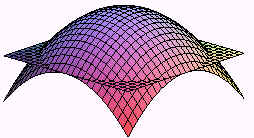
Solution

We calculate partial derivatives

        f_x(x,y)  =  -2x            f_y(x,y)  =  -2y

so that 

        1 + f_x²(x,y)  + f_y²(x,y)  =  1 + 4x² + 4y² 

At this point if we listen closely, we should hear a little voice pleading "Polar Coordinates".  We listen to its call and realize that the region is just the circle 

        r  =  5

Now convert the integrand to polar coordinates to get

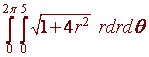
Now let

        u  =  1 + 4r²         du  =  8rdr

and substitute

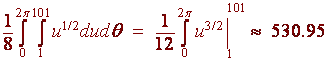
Back to the Multiple Integration Home Page

Back to the Vector Calculus Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions