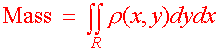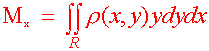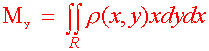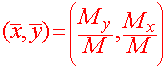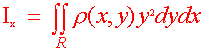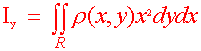Center of Mass and Moment of Inertia

Mass

We saw before that the double integral over a region of the constant function 1 measures the area of the region.  If the region has uniform density 1, then the mass is the density times the area which equals the area.  What if the density is not constant.  Suppose that the density is given by the continuous function 

        Density  =  r(x,y)

In this case we can cut the region into tiny rectangles where the density is approximately constant.  The area of mass rectangle is given by 

        Mass  =  (Density)(Area)  =  r(x,y) Dx Dy 

You probably know where this is going.  If we add all to masses together and take the limit as the rectangle size goes to zero, we get a double integral.

Example

A rectangular metal sheet with 2  <  x  < 5  and  0  <  y  <  3 has density function 

        r(x,y)  =  x + y

Set up the double integral that gives the mass of the metal sheet.

Solution

We just have the integral

Moments and Center of Mass

We have seen in first year calculus that the moments about an axis are defined by the product of the mass times the distance from the axis.  

        M_x  =  (Mass)(y)        M_y  =  (Mass)(x)

If we have a region R with density function r(x,y), then we do the usual thing.  We cut the region into small rectangles for which the density is constant and add up the moments of each of these rectangles.  Then take the limit as the rectangle size approaches zero.  This will give us the total moment.  

Example

Set up the integrals that give the center of mass of the rectangle with vertices (0,0), (1,0), (1,1), and (0,1) and density function proportional to the square of the distance from the origin.  Use a calculator or computer to evaluate these integrals.

Solution

The mass is given by 

The moments are given by 

These evaluate to 

        M_x  =  5k/12        and       M_y  =  5k/12

It should not be a surprise that the moments are equal since there is complete symmetry with respect to x and y.  Finally, we divide to get

        (x,y)  =  (5/8,5/8)

This tells us that the metal plate will balance perfectly if we place a pin at (5/8,5/8)

Moments of Inertia

We often call M_x and M_y the first moments.  They have first powers of y and x in their definitions and help find the center of mass.  We define the moments of inertia (or second moments) by introducing squares of y and x in their definitions.  The moments of inertia help us find the kinetic energy in rotational motion.  Below is the definition

Exercise 

Find the moments of inertia for the previous square metal plate.

Back to the Multiple Integration Home Page

Back to the Vector Calculus Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions