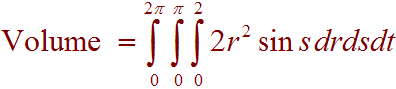Math 202 Practice Final

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your Work

Problem 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true, explain why.

A.  Let Q be a three dimensional solid and let 

        F(x,y,z)  =  (x²y + sin z)i+ (cos x - xy²)j + (3xy + z)k

and let S be the boundary of Q with outwardly pointing normal.  The the volume so Q is given by

Solution

True,

We have

        divF  =  2xy - 2xy + 1  =  1

Using the divergence theorem, we see that 

which is just the volume of the solid.

B.  Let F  =  3xy i + cosx j and let C₁ and C₂ be as shown below.  Then

Solution

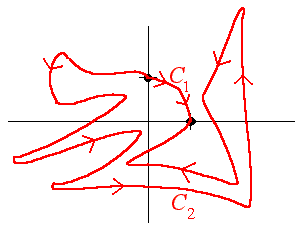
False for many reasons.  First, F is not conservative.  Hence even if the other issue was not there, this would be false.  Second, Green's Theorem needs Fodr, not FoNdr.

C.  A new particle, the fluxon, has been discovered to be emitted from the sun.  The particle emits a force field 

        F(x,y,z)  =  (y² - z) i + (x² - z) j + (x² + y²) k

where the origin represents the center of the sun.  If the total flux through the earth's northern hemisphere has been calculated as 10,000, then the total flux through the earth's southern hemisphere must also be 10,000.

Solution

False,  since divF  =  0, the total flux must be zero.  If the flux through the northern hemisphere is 10,000, then the flux through the southern hemisphere must be -10,000.

Problem 2  You are the captain of the spaceship Potential that you have programmed to follow the vector-valued function 

        r(t) =  (t² + 5) i + (t - 3) j + t³ k 

where t is measured in hours.  However, at time t  =  2, your engines fail and your ship begins drifting in deep space.  There is a deep space station located at (6,2,38).  

A.  Find the vector-valued function that describes the Potential's flight after the engines failed. Use t  =  2 to represent the time at which your engines first shut down. (Hint:  This should be a linear vector valued function.)

Solution

The flight will go in a linear path in the direction of the unit tangent vector with speed equal to the speed when the engines fail.  We have

        r'(t)  =  2t i + j + 3t² k

        r'(2)  =  4i + j + 12k

When t  =  2, the spacecraft is at 

        r(2)  =  9i - j + 8k 

The flight can be described by

        r_f(t)  =  r(2) + (t - 2)r'(2)  =  9i - j + 8k + (t - 2)(4i + j + 12k)

        =  (1 + 4t)i + (-3 + t)j + (-16 + 12t)k 

B.  Will your ship make it to the station, or will you float helplessly for eternity?

Solution

We are looking for a time t with 

        r_f(t)  = 6i + 2j + 38j

Setting the j components equal we get

        -3 + t  =  3        t  =  5

However

        r_f(5)  =  9i + 2j + 44k

since the i and k components of r_f and the station are different, we can conclude that our spaceship will drift away to eternity.

Problem 3  Show that the helix

        r(t)  =  (R cos t) i + (R sin t) j + t k 

where R is a positive constant, has the property that N(t) ^. r(t) is a constant.  Find this constant.

Solution

We first calculate T(t)

        r'(t)  =  (-R sin t) i + (R cos t) j + k 

        || r'(t)||  =  (R² sin² t + R² cos² t + 1)^1/2  =  (R² + 1)^1/2

Hence 

        T(t)  =  (R² + 1)^-1/2 [(-R sin t) i + (R cos t) j + k]

Next, we have

        T'(t)  =  (R² + 1)^-1/2 [(-R cos t) i + (-R sin t) j]

and

        ||T'(t)||  =  (R² + 1)^-1/2 [R² cos² t + R² sin² t]^1/2  =   (R² + 1)^-1/2 [R] 

Dividing gives

        N(t)  =  -cos t i - sin t j

Finally, we take the dot product

        N(t) ^. r(t)  =  [(R cos t) i + (R sin t) j + t k] ^. [-cos t i - sin t j]

        =  R cos² t + R sin² t  =  R

Problem 4  The probability density function for an event is given by

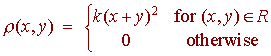
where R is the square with vertices (4,0), (6,2), (4,4), and (2,2).

A.  Use the appropriate change of variables (Jacobians) to find k that is solve 

Solution

We sketch the picture and find the equation of the four lines that border the square.

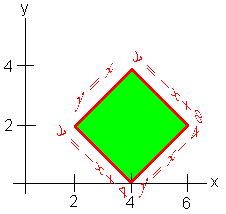
We can also write

        0  <  x - y  < 4        and        4  <  x + y  <  8

We let 

        u  =  x - y        v  =  x + y

Adding the two equations gives

        u + v  =  2x        x  =  1/2 (u + v)

Subtracting the two equations gives

        v - u  =  2y        y  =  1/2 (v - u)

We can compute the Jacobian

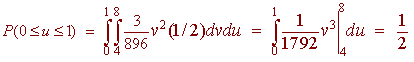
We have

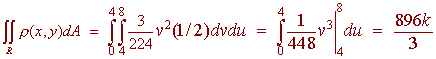
Setting this equal to 1 gives

                    3
        k  =                    
                  896

B.  Find the probability that  0  <  x - y  <  1

Solution

Since

        u  =  x - 1

we just adjust the limits appropriately

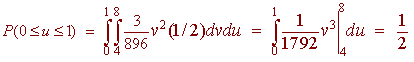
Problem 5  Switch the order of integration and write as one double integral

Solution

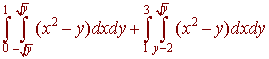
The key to this problem is to sketch the picture which is shown below

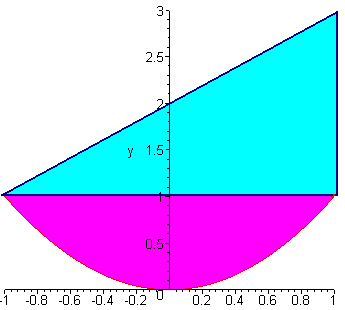
Now we can realize the region as being bounded from below by y  =  x² and above by y  =  x + 2.  We have

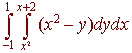
Problem 6  Set up the integrals that give the following.  Use the most appropriate coordinate system.

A.  The mass of the solid that lies inside the sphere

        x² + y² + z²  =  9

and outside the cone

        z²  =  x² + y² 

that has density function

Solution

We use spherical coordinates.  The sphere becomes

        r  =  3

and to find the equation of the cone, we add z² to both sides to get

        2z²  =  x² + y² + z² 

        2r²cos² f  =  r²         cos² f  = 1/2        f  =  p/4

Now we can write

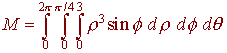
B.  The surface area of the part of the paraboloid 

        z  =  x² + y²

that lies inside the cylinder

        x² + y²  =  4

Solution

We calculate the partials

        z_x  =  2x        z_y  =  2y        (1 + z_z + z_y)^1/2  =  (1 + 4x² + 4y²)^1/2

Since the region is a circle of radius 2, we convert to polar coordinates to get

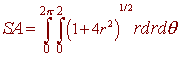
Problem 7  Find the work done by the force field 

        F(x,y)  =  (3x² - y) i + (x² - y³) j

as a particle moves counterclockwise around the rectangle with vertices (2,1), (5,1), (5,5), and (2,5).

Solution

We use Green's Theorem.  We have

        N_x - M_y  =  2x + 1

We have

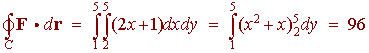
Problem 8

Verify Stokes Theorem where 

        F(x,y,z)  =  (2x) i + (2y) j + (z sin z³) k

and S is part of the paraboloid 

        z  =  9 - x² - y² 

that lies above the plane z  =  8 oriented upward.

Solution

We first compute the line integral 

We notice that the intersection of the paraboloid and the plane is given by 

        9 - x² - y²  =  8        x² + y²  =  1

This is the circle of radius 1 raised 8 units above the xy-plane.  Its parameterization is given by

        r(t)  =  (cos t) i + (sin t) j + 8k 

        r'(t)  =  (-sin t) i + (cos t) j  

so that 

        F ^. dr  =  [(2cos t) i + (2sin t) j + (8 sin 8³) k] . [(-sin t) i + (cos t) j]

        =  -2 sin t cos t + 2 sin t cos t  =  0

Since the integrand is zero, so is the integral.

Now we use Stokes Theorem.  We have 

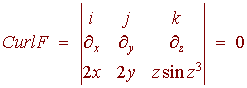
So that the surface integral is zero.

Problem 9

Use the transformations

S(u,v,w):  x(u,v,w) = u - v + w, y(u,v) = v+w, z(u,v,w) = 2w

and

T(u,v,w):  u(r,s,t) = rsin(s)cos(t), v(r,s,t) = rsin(s)sin(t), w(r,s,t) = rcos(s)

To represent the volume of the solid inside of

(x + y - z)² + (y - z/2)² + (z/2)²  =  4

Thus under S, the solid becomes

u² + v² + w²  =  4

Next, note that the transformation T is just spherical coordinates.  Thus the limits are

0 < r < 2,     0 < s < p,     0 < t < 2p

Since we are finding the volume, the integrand is just the Jacobian.  We have

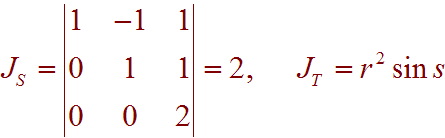
and

J_SoT = J_SJ_T

Putting this all together gives