Math 202 Practice Midterm 3

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

Printable Key

Problem 1  Please answer the following true or false.  If false, explain why or provide a counter example.  If true explain why.  

A.  Let f(x,y,z) be a function with continuous second order partial derivatives and let F(x,y,z) be the gradient of f(x,y,z).  If S is the ellipsoid 

            x²  
                    +  y² + z²  =  1
            4

oriented outward, then 

Solution

B.  Let F(x,y) be a conservative vector field, then

Solution

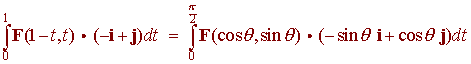
Problem 2

Show that 

for any closed surface S.  

Solution

Problem 3

A fish starting at the origin swims in a straight path to the point (0.2,0.1,0.3), then changes direction and swims along the circular path through the point (0.5,0.2,0.6) and the point (0.7,0.5,0.8), and finally changes directions heading straight to the point (1.5,1,2).  The current can by represented by the vector field

        F(x,y,z)  =  (2x + 2z)i + (1 - 3z)j + (2x - 3y + 5)k

Find the total work done by the current.

Solution

Problem 4

Evaluate where F is the vector field 

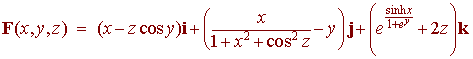
and S is the rectangular solid with vertices (0,0,0), (1,0,0), (1,2,0), (0,2,0), (0,0,3), (1,0,3), (1,2,3), (0,2,3).

Solution

Problem 5

Find the work done by sailing a ship from the point (2,3) the the point (-1,2) against the wind with velocity field

        F(x,y)  =  yi + (3x + 2y)j

Solution

Problem 6

Find the flux of F through the surface S where 

        F(x,y,z)  =  3zi - 4j + yk

and S is the part of the plane

        x + y + z  =  1

in the first octant with upwardly pointing unit normal.