MATH 202 MIDTERM 1
Please work out five of the given
six problems and indicate which problem you are omitting.
Credit will be based on the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Please answer the following true or false. If false, explain why or provide a counter example. If true explain why
A) (12 Points) If r(t) is parameterized by arclength, then a and N are parallel.
True, since
s(t) = t
We have
s''(t) = 0
So that
a = s''(t)T + k(s')2N = k(s')2N
so that a and N are multiples of each other. Hence they are parallel.
B) (13 Points) If r(t) is a differentiable vector valued function then
![]()
False, for example if
r(t) = i + t j
then
![]()
and
||r'(t)|| = || j || = 1
So they are different.
PROBLEM 2 (25 Points)
Let
r(t) = 2t i - 4t2 j
- Find T(-1).
We have
r'(t) = 2 i - 8t j
so that
![]()
Now just plug in -1 for t to get
![]()
- Find N(-1).
Use the quotient rule to get
![]()
Now get rid of the denominator and multiply by the root to get
(-4j)(1 + 16t2) - (i - 4tj)(16t)
= 4[-j(1 + 16t2) - (i - 4tj)(4t)]
Now divide by 4 and plug in -1 for t to get
-17 j - (i + 4j)(-4) = 4i - j
Dividing by the magnitude gives
![]()
- Find the
equation of the circle of curvature for r(t)
at t = -1.
The acceleration vector is
a = r''(t) = -8j
Dotting with the normal vector gives the component of the acceleration in the direction of the normal vector. We get
aN =
![]()
and
(ds/dt)2 = ||r'(t)||2 = 1 + 64t2
evaluating at t = -1 gives
65
Using the curvature formula gives
65K = an
so that
![]()
The radius of the circle is just the reciprocal of the curvature.
To find the center, we add the vectors
Center = r(-1) + KN
which gives
![]()
Call this
ai + bj
Then the equation of the circle is just
(x - a)2 + (y - b)2 = 1/K2
PROBLEM 3 (25 Points) Jason Elam (the football kicker for the Denver Broncos) can kick a football with an initial velocity of 60 feet per second. At what angle should the ball be kicked to maximize the horizontal distance that the ball travels before it lands on the ground? (Use vectors please).
The acceleration is
a(t) = -32 j
Integrating gives
v(t) = vx i + (-32t + vy) j = 60cosq i + (-32t + 60sinq) j
Now integrate again to get
r(t) = 60t cosq i + (-16t2 + 60sinq t) j
Notice that these constants are all zero since the ball starts at the origin. The ball will reach its maximal horizontal distance when the j component equals 0. We have
-16t2 + 60sinq t = 0
t = 15/4 sinq
Now plug back into the i component and maximize
h = 60 (15/4 sinq) cosq = 225/2 sin(2q)
Now to maximize, we take the derivative and set it equal to zero
h' = 225 cos(2q)
This is zero when q = p/4.
PROBLEM 4 (25 Points) Prove
the following theorem:
Let r(t) be a differentiable vector valued function, then
|(r x v) . a| = ||r'|| ||aN|| |r . (T x N)|
Since
v = ||r'|| T
we have
|(r x v) . a| = |(r x ||r'||T) . a| = |(r x ||r'||T) . (aTT + aNN)|
= ||r'|| |(r x T) . aTT + (r x T) . aNN)|
Since (r x T) is orthogonal to T, the first term is zero. We get
= ||r'|| |(r x T) . aNN)| = ||r'|| |aN| |(r x T) . N)|
PROBLEM 5 (25 Points)
Find the parametric equations of the tangent line to the curve that is formed by intersecting the sphere x2 + y2 + z2 = 2 and the plane x + y - z = 2 at the point (1,1,0).
grad F = 2x i + 2yj + 2z k and grad G = i + j - k
Evaluating these at the point (1,1,0) gives
n1 = 2 i + 2 j and n1 = i + j - k
The cross product is
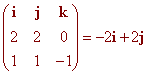
Now we use the formula for a line given a point and a parallel vector
r(t) = i + j + t(-2i + 2j)
The parametric equations are
x(t) = 1 - 2t y(t) = 1 + 2t z(t) = 0
PROBLEM 6 (25 Points)
If
a(t) = t i + j - k
find r(5) if
r(0) = i - k
and
r(1) = j +
We integrate to get the velocity function
v(t) = (1/2 t2 + vx )i + (t + vy )j + (-t + vz )k
Integrate again to get
r(t) = (1/6 t3 + vxt + rx)i + (1/2 t2 + vyt + ry)j + (-1/2t2 + vzt + rz )k
Now plug in the first initial condition to get
rx i + ry j + rz k = i - k
So that
rx = 1 ry = 0 rz = -1
Plugging these in and using the second initial condition gives
(1/6 + vx + 1)i + (1/2 + vy)j
+ (-1/2 + vz - 1)k = j +
So that
vx = -7/6 vy = 1/2 vz = 5/2
Substituting gives
r(t) = (1/6 t3 - 7/6 t + 1)i + (1/2 t2 + 1/2 t)j + (-1/2t2 + 5/2 t - 1)k
Now plug in 5 to get
r(5) = (125/6 - 35/6 + 1)i + (25/2 + 5/2)j + (-25/2 + 25/2 - 1 )k
= 16 i + 15 j - k
Extra Credit: Write down one thing that your instructor can do to make the class better and one thing that is going well.
(Any constructive remark will be worth full credit)