Tony Jones

Larry Green

Math 201

3-12-04

Before Warm Up Stretching Vs. After Warm Up Stretching

 

My project takes place in a martial arts studio in Incline Village, Nevada. I wanted to know if a ten-minute warm up is in fact related to an increase in stretch. A warm up obviously reduces the risk of injury, but does it actually increase the range of stretch. Many students have noticed their greatest results without a warm up. They claim it is because their muscles are still fresh and unused which enables them to attain maximum flexibility. I took a convenience sample of thirty-two Taekwon-do students of various experience levels. I put each student on a stretching machine to record the maximum stretch (in degrees). This was done at the time each student walked in the door and after a rigorous ten-minute warm up. The warm up consisted of each student breaking a sweat and a lot of motion drills with the legs. The null hypothesis is that there is no difference between a cold stretch and a warm stretch. The alternate hypothesis is that the stretch after the warm up is greater than the stretch before the warm up.  My secondary null hypothesis is that there is no correlation before warm up stretching and after warm up stretching. The alternate hypothesis is that there is a relationship with before warm up stretching and after warm up stretching. I labeled the before warm up stretch in the X- axis and the after warm up stretch in the Y- axis for the correlation and regression charts.

 The following chart summarizes the statistics of my project. The sample means in the before and after cases are very close to one another. This interpretation shows that there was not a large difference between each student’s stretch. When comparing the minimum and maximum results, it is apparent that the warm up had the highest stretch. The standard deviation in both cases explains why the data is so spread out. The medians are also similar. By looking at this chart it is hard to make any conclusions since the data are very similar.

 

Summary statistics

Column	n	Mean	Variance	Std. Dev.	Std. Err.	Median	Range	Min	Max	Q1	Q3
After Warm Up	32	125.65625	295.2006	17.181402	3.0372717	119.5	61	103	164	112.5	134
Before Warm Up	32	125.34375	292.49094	17.102365	3.0232997	120	58	104	162	111.5	137

 

 

Since I used pairing in a before and after test, the following data will help me determine if I can reject the null hypothesis and accept the alternate hypotheses or fail to reject the null hypothesis at a 5% level of significance.

            Paired T-test results:
 _D - mean of the differences between After Warm Up and Before Warm Up
H₀: _D = 0
H_A: _D > 0

Difference	Sample Diff.	Std. Err.	DF	T-Stat	P-value
After Warm Up - Before Warm Up	0.3125	0.41745558	31	0.74858266	0.2299

 

 I wanted to see if a warm up would increase the stretch. I subtracted the before warm up stretch from the after warm up stretch to get the difference. I then observed the P-value and found that it was greater than .05. After viewing this data I came to the conclusion that there is not enough evidence to make such a claim. So I failed to reject the null hypothesis and concluded that more information needs to be gathered in order to accept the alternate hypothesis at the 5% level. Put another way, there is not enough evidence to conclude that a warm up will necessarily increase a stretch.

            The next set of charts show the confidence intervals for the means.

95% Confidence interval results:
  - mean of Variable

Variable	Sample Mean	Std. Err.	DF	L. Limit	U. Limit
Before Warm Up	125.34375	3.0232997	31	119.17769	131.50981

 

 

95% Confidence interval results:
  - mean of Variable

Variable	Sample Mean	Std. Err.	DF	L. Limit	U. Limit
After Warm Up	125.65625	3.0372717	31	119.46169	131.8508

 

95% Confidence interval results:
 _D - mean of the difference between after Warm Up and Before Warm Up

Difference	Sample Diff.	Std. Err.	DF	L. Lim	U. Lim
After Warm Up - Before Warm Up	0.3125	0.41745558	31	-0.5389063	1.1639062

 

The first chart in this series says that with 95% confidence, the mean stretch (in degrees) before warm up is between 119.2 and 131.5 degrees. The second chart gives a 95% confidence interval for the mean stretch (in degrees) after a warm up is between 119.5 and 131.9 degrees. The final chart of this series indicates the difference of means. With 95% confidence, I can say that the after warm up is smaller than the before warm up by no more than .5 degrees. I can also say that the after warm up is greater than the before warm by no more than 1.16 degrees.           

The following stem and leaf display shows the distribution of the data.

Variable: After Warm Up

10 : 34

10 : 69

11 : 0012334

11 : 66789

12 : 02

12 : 69

13 : 01444

13 :

14 :

14 : 66

15 : 003

15 :

16 : 14

 

Variable: Before Warm Up

10 : 44

10 : 678

11 : 0012234

11 : 7789

12 : 14

12 : 599

13 : 1

13 : 677

14 : 3

14 : 568

15 :

15 : 5

16 : 12

 

 Both sets are skewed to the right and are unimodal. The stem and leaf display helps to visualize the data spread. There are three gaps in the after warm up display and only one gap in the before warm up display. The 110 to 130 degree categories contain the most number of data. The before warm up stem and leaf appears to be more consistent. The data in this display appears to be quite similar. Again, by observing this display, it is difficult to find any major differences.

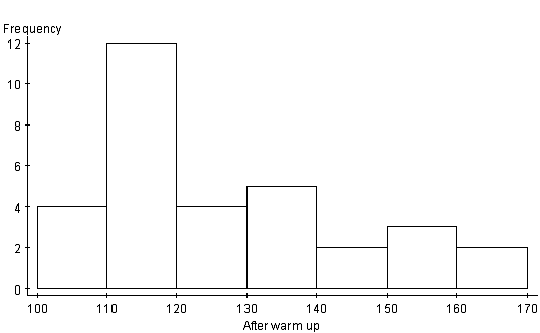
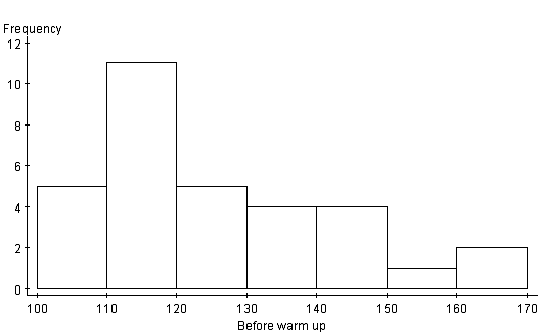
            The histograms below give another perspective for the data distribution. Both histograms are unimodal. This means that most students fell into the 110 to 120 degree category. Both histograms are also skewed to the right. As the degrees on the stretching machine got higher, the number of students in this category decreased. It is hard to make

any conclusion from these graphs, but it appears that the after warm up has a slightly higher top end.

 

 

 

 

 

 

 

 

 

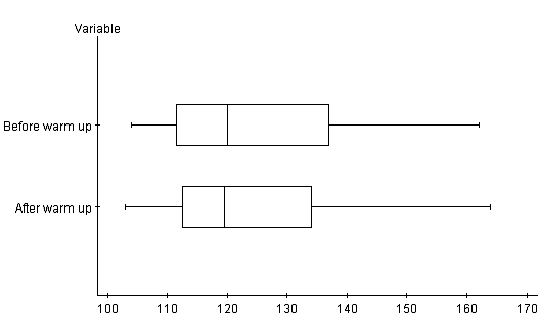
            The box and whisker plots below do a great job in capturing that data spread to be interpreted. The after warm up box and whisker plot has  the smallest and highest values of outliers. The interquartile range of the before warm up box and whisker is larger. This suggests more data was clustered about the median. These boxes indicate where the middle half of the data lies. Half the students in the before warm up category stretch between 111 and 139 degrees. Half the students in  the after warm up category stretch between 112 and 137 degrees. This means that the after warm up does have some higher increases, but it is not consistent enough to make a conclusion regarding which one gives better results.

 

 

 

 

 

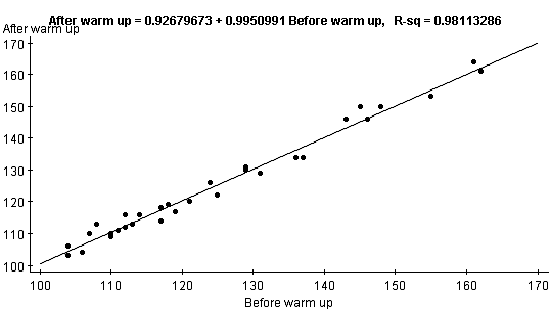
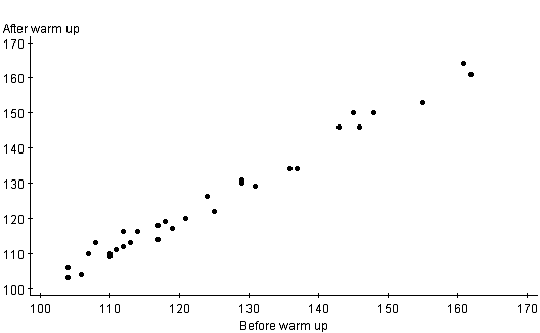            Finally I wanted to test my secondary hypothesis. The null hypothesis is that there is no correlation between before warm up stretching and after warm up stretching. The alternate hypothesis is to see if there is a correlation between the two. In referring to the scatter diagram below, there is a definite high positive correlation. The R-value is .99, which is very close to one. It is evident that the after warm up stretch stays consistent with the before warm up stretch. I can reject the null hypothesis and can say that there is enough evidence to conclude that there is a correlation between before warm up stretching and after warm up stretching. A change in stretch either up or down is very subtle according to the high correlation between the two. By observing this chart and the previous charts, it is apparent that the fluctuation in degrees of stretching will be very small. A student who is not limber will not be able to do the splits after a ten minute warm up. Similarly, a student who is limber will still be limber after a ten minute warm up.

 

 

 

   The last chart in my project is the simple linear regression display. It is going to tell me how strong my correlation will be. It will also tell me if I can make any predictions about after warm up stretching by plugging in a before warm up value. My R-squared value of .98 indicates that I can make a strong prediction.  By observing the below data, I can see the error of estimate is low which means I have a strong correlation. With such a strong correlation, the simple linear regression data will be a good predictor to get Y From X. To test my prediction I chose 115 degrees. The slope of the line is noted on the bottom most chart. The slope says, that for every increase in a degree before a warm up will correlate to a one degree increase after the warm up.  By observing the charts, I can be 95% confident that if a student stretches at 115 degrees before the warm up, he or she will stretch between 114 and 116 degrees after the warm up. Since the hypothesis test lacks sufficient evidence to conclude that a warm up constitutes a greater stretch, I can predict that the degrees after the warm up will differ very slightly (either up or down) from the before warm up stretch.