THE NUMBER OF HOURS LTCC STUDENTS SPEND ON THE COMPUTER DOING SCHOOLWORK IS NOT AN INDICATOR OF THE NUMBER OF HOURS THEY SPEND ON THE COMPUTER FOR PERSONAL USE.

In this day and age, people use the computer for everything from communication and research, to shopping, banking and paying the bills. Being a student who spends a lot of time on the computer doing much of my schoolwork, I often feel that after the bulk of my work is done, I have little or no interest in spending more time e-mailing and surfing the net. I was curious to find out if other students at LTCC shared the same level of interest in the computer as I do. I predict that students spend more time on the computer doing schoolwork than for personal interest. Therefore, H0: u1-u2 = 0 and H1: u1-u2 > 0, where u1= the amount of hours a student spends on a computer doing schoolwork, and u2= the amount of hours a student spends on the computer for personal interest. I also predict a negative correlation between the number of hours a student spends on the computer for schoolwork and the number of hours spent on the computer for personal interest, with H0: r=0, and H1: r>0.  I took a convenience sample of n=31 LTCC students two weeks before finals because my time was limited, the sampling type was sufficient for my project, and the sample size greater than 30 enabled me to use the central limit theorem for normal distribution. There is some bias with surveying LTCC students because computers are readily available throughout the campus and many students have heavy amounts of schoolwork at this point in the quarter. Each person in the sample was asked two questions: “How many hours each week do you spend on the computer doing schoolwork?” and “How many hours each week do you spend on the computer each week for personal use?” These questions provided the data I needed to conduct the statistical survey. Because only 95% accuracy was needed for a survey such as this, I used a 5% significance level. With the help of www.statcrunch.com, the following graphs, tables, and calculations are shown below.

Summary statistics

This table summarizes the sample results. With this table I can conclude that for the mean amount of hours a student spends on the computer for schoolwork is ~ 3.7 with a standard deviation of~1.9 with a low variance. With the mean at 3.7 and the median at 3, I can conclude that the binomial distribution is normal and symmetrical. With Q1 at 2 and Q3 at 5, the inter-quartile range for schoolwork hours spent on the computer is 3.The mean amount of hours spent on the computer for personal use is ~3.0 with a standard deviation of  ~1.9 with a low variance. With the mean at 3 and the median at 2, the distribution here is close to normal and symmetrical. With Q1 at 2 and Q3 at 4, the inter-quartile range for personal hours spent on the computer is2.

95% Confidence interval results:
m - mean of Variable

This table shows with 95% confidence, that the mean number of hours that students at LTCC spend on the computer for schoolwork is between 2.9 and 4.4, and that the mean number of hours a student spends on the computer for personal use is between 2.19 and 3.6.

 

95% Confidence interval results:
m_D - mean of the difference between schoolwork and personal

This table depicts the confidence interval of the mean difference between the number of hours LTCC students spend on the computer and the number of hours LTCC students spend on the computer for personal use. Since the mean difference is between -0.5 and 1.79, I can conclude with 95% confidence that schoolwork hours spent on the computer is less than personal hours spent on the computer by no more than 0.50 and personal hours spent on the computer is greater than schoolwork hours spent on the computer by no more than 1.79. This conclusion would not support my initial hypothesis but to further clarify the confidence interval, the hypothesis test is shown on the table below.

Paired T-test results:
m_D - mean of the differences between schoolwork and personal
H₀:m_D = 0
H_A:m_D > 0

To be sure the data was valid at the 95% confidence level, a test was conducted at the 0.05 significance level. The P-value is an indicator on whether to reject or fail to reject the null hypothesis. The 0.129 P-value for this test is much greater than the 0.05 significance level and with 95% significance, I will fail to reject the null hypothesis. Therefore, there is not enough statistical evidence to prove that LTCC students spend more hours on the computer doing schoolwork than for personal use.

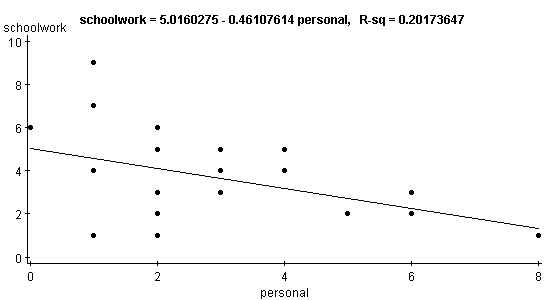
Simple linear regression results:
Dependent Variable: schoolwork
Independent Variable: personal

Sample size: 31
Correlation coefficient: -0.4492
Estimate of sigma: 1.808153

My hypothesis was that the amount of hours LTCC students spend on the computer for schoolwork would be a predictor to the number of hours LTCC students spend on the computer for personal use. The simple linear regression provides information about the coefficient of correlation=r and what predictions can be made from the data. I chose schoolwork for the y-value (dependent variable) and personal use for the x-value (independent variable) to see if there is a correlation between the two. The r-value = -.3258, and the negative value indicates a negative or downward trend. The regression line: schoolwork = 4.748882- 0.3533463 x (personal) also indicates a downward slope and shows that there is a weak correlation between the amount of hours LTCC students spend on the computer for schoolwork and the amount of hours LTCC students spend on the computer for personal use. Since the P-value for the regression line = 0.0737 and this number is greater than the 0.05 significance level, I can conclude with 95% significance that there is little or no correlation between the number of hours LTCC students spend on the computer for schoolwork and the number of hours LTCC students spend on the computer for personal use and fail to reject the null hypothesis. The r-squared-value is 0.106 and because it is numerically close to zero, this indicates no linear pattern. From the scatter plot it is clear that the amount of hours LTCC students spend on the computer for schoolwork is not an indicator of the number of hours LTCC students spend on the computer for personal use. To get the percentage of variation, r-squared is multiplied by 100. Only 10% in variation in hours LTCC students spend on the computer for schoolwork can be predicted by the variation of number of hours LTCC students spend on the computer for personal use. 90% is unpredictable at the 0.05 significance level. It is important to remember that simply because LTCC students spend much time on the computer doing schoolwork, does not imply that students will not spend time surfing the net and e-mailing.

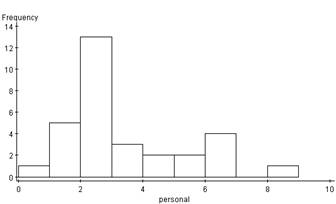
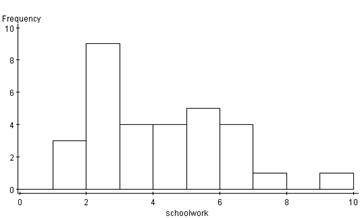
HISTOGRAMS

The histograms provide a quantitative analysis of the data. The personal hours histogram is uni-modal and skewed right with the highest frequency at 2 hours. This depicts that most LTCC students who used the computer for personal reasons used the computer 2 hours. There is also an outlier at 8 hours meaning that of the 31 students surveyed, none used the computer 7 hours. The schoolwork histogram is also uni-modal and skewed right with the highest frequency at 2 hours. Like the personal hours spent on the computer, most students spent 2 hours on the computer doing schoolwork. There is an outlier at 10 hours meaning that of the 31 students surveyed, none used the computer for schoolwork for 9 hours.  By simply glancing at the two histograms in comparison, they show very similar trends, that LTCC students spend close to the same amount of hours on the computer for personal as well as schoolwork.  

Stem and Leaf

Variable: school work

1 : 000                                                                                      

1 : 

2 : 000000000

2 : 

3 : 0000

3 : 

4 : 0000

4 : 

5 : 00000

5 : 

6 : 0000

6 : 

7 : 0

7 :      

8 : 

8 : 

9 : 0

Variable: personal

1 : 0000

1 : 

2 : 00000000000000

2 : 

3 : 0000

3 : 

4 : 00

4 : 

5 : 00

5 : 

6 : 0000

High: 8

The stem and leaf display helps to visualize the data distribution and can be compared to the histogram. In the schoolwork stem and leaf, again, the highest frequency is at 2 with an outlier at 8. The personal stem and leaf the highest frequency is at 2 with an outlier at 8. The stem and leaf displays are both skewed right.

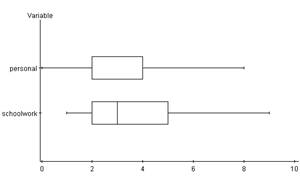
Boxplot

The box-plot displays the data’s highest value and the data’s lowest value Q1, and Q3 with the line in the box indicating the median. There is a larger inter-quartile range for schoolwork. While both lines are at about 3. This indicates that. While the median is numerically comparable, there is more variance and spread for inter-quartile range in the number of hours spent doing schoolwork on the computer.

In conclusion, the amount of hours LTCC students spend on the computer for schoolwork does not predict the amount of hours spent on the computer for personal use. In fact, the average amount of hours is about equal to the other. In doing a convenience sample, I was limited to the daytime students giving rise to several biases such as the school load of daytime students as opposed to nighttime students, school load during finals week, and seasonal outdoor activities. This study in no way represents LTCC students as a whole; a larger sample would supply greater accuracy.