Brendan Couvreux

Instructor Larry Green

Math 201

18 March 2003

The Project

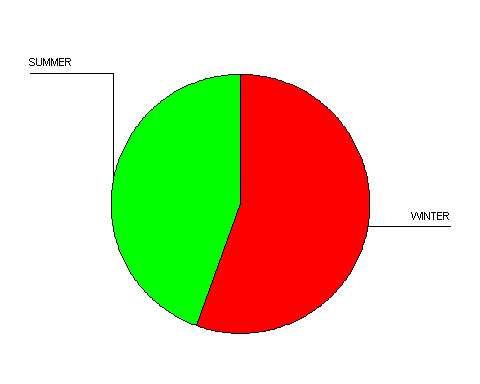
            I surveyed 51 professional ski patrollers at Heavenly mountain resort and asked, on average, how many days they worked during the winter season and how many days they worked during the summer. Convenience sampling was used for this survey. Considering the fact that the 51 patrollers surveyed comprise almost the entire population of the professional ski patrol members at Heavenly ski resort, the results of this test can be used to represent the majority of professional ski patrollers in the Lake Tahoe Basin. The pie chart represents the proportion of days worked during the winter and days worked during the summer.

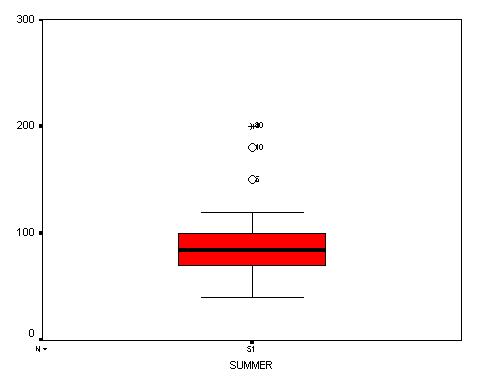
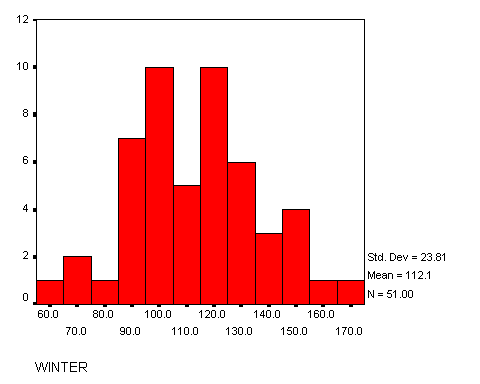
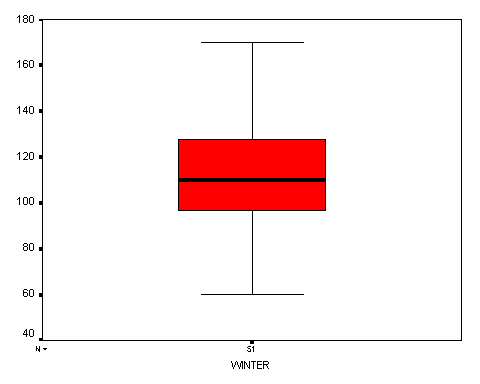
            It is observed that the average number of days worked during the winter is 112 days with a standard deviation of approximately 24 days. With a 95% confidence, we can say that the average number of days that a patroller works during the winter is between 105 days and 119 days. The median number of days worked during the winter for patrollers is 110 days. The 5% trimmed mean (meaning 5% of the data was eliminated at both ends in an effort to minimize outliers) for the number of days worked during the winter is 112 days. The minimum number of days worked during the winter is 60 days and the maximum is 170 days. There is a total range (from the minimum to the maximum number of days worked during the winter) of 110 days. The interquartile range (the difference between the 75^th percentile and the 25^th percentile) is 35 days for winter. The Box plot illustrates the maximum and minimum with the two “whiskers.” The bottom of the box represents the 25^th percentile and the top of the box represents the 75^th percentile. The line in the middle represents the median. The bar chart for winter illustrates the quantity of patrollers that worked 0-60 days, 61-70 days, 71-80 days, 81-90 days, 91-100 days, 101-110 days, 111-120 days, 121-130 days, 131-140 days, 141-150 days, 151-160 days, and 161-170 days.

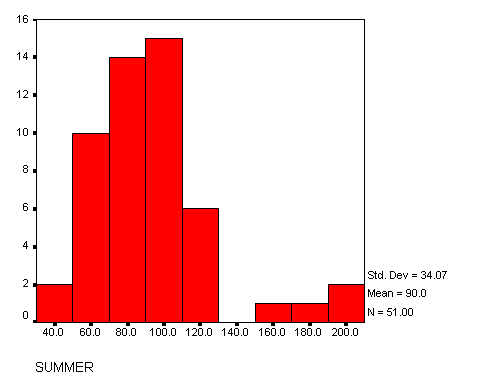
The average number of days worked during the summer is 90 days with a standard deviation of approximately 34 days. With a 95% confidence, we can say that the average number of days that a patroller works during the summer is between 80 days and 100 days. The median number of days worked during the summer for patrollers is 85 days. The 5% trimmed mean (meaning 5% of the data was eliminated at both ends in an effort to minimize outliers) for the number of days worked during the summer is 87 days. The minimum number of days worked during the summer is 40 days and the maximum is 200 days. There is a total range (from the minimum to the maximum number of days worked during the summer) of 160 days. The interquartile range (the difference between the 75^th percentile and the 25^th percentile) is 30 days for summer. The bar chart for summer illustrates the quantity of patrollers that worked 0-40 days, 41-60 days, 61-80 days, 81-100 days, 101-120 days, 121-140 days, 141-160 days, 161-180 days, and 181-200 days.

With this data I have tested the hypothesis that patrollers work more days during the winter than they do during the summer: H₀: m=0     H₁:m>0  a=0.05 The resulting p value is 0.026. P is inferior to a, thus we reject H₀ and accept H₁. This means that with a 5% level of significance, Heavenly professional ski patrol members work more days during the winter than they do during the summer. The average difference between the number of days worked during the winter and summer is approximately 22 days with a standard deviation of 47 days. With a 95% confidence, we can say that Heavenly professional ski patrollers work between 9 and 35 days more during the winter than they do during the summer.

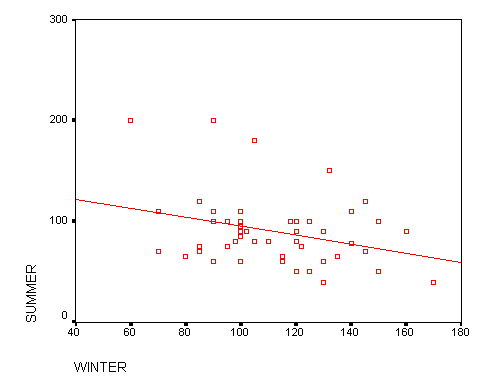
I have also tested the hypothesis that the more days patrollers work during the winter, the less days they will work during the summer: H₀: R=0  H₁: R<0  It is observed that the value of R is –0.311 and R²=0.097 with a standard error of estimate S_E=22.86. This means that 9.7% of the variations of the number of summer days worked is explained and 90.3% of the variations of the number of summer days worked is unexplained. We observe here a low correlation showing little relation between the number of days worked during the winter and number of days worked during the summer. The scatter diagram represents the number of days that each patroller works during summer and winter. The x axis being the number of days worked during the winter and the y axis being the number of days worked during the summer. The equation of the regression line is: y=131.651-0.217x. –0.217 is the slope of the regression line and 131.651 is the y intercept.